2.1. Đường tiệm cận ngang
a) Định nghĩa
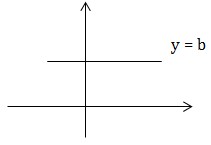
- Đường thẳng \(y=b\) được gọi là tiệm cận ngang của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau:
+ \(\lim_{x\rightarrow -\infty } f(x) = b\)
+ \(\lim_{x\rightarrow +\infty } f(x) = b\)
b) Chú ý
- Điều kiện để đồ thị hàm số \(y = \frac{P(x)}{Q(x)}\) có tiệm cận ngang là bậc của đa thức P(x) bé hơn hoặc bằng bậc của đa thức Q(x).
- Tổng quát: Xét hàm số \(y = \frac{a_nx^n + ... + a_0}{b_mx^m + ... + b_0} \ \ \ m, n \in N; a_n\neq 0; b_m\neq 0\).
+ Điều kiện để hàm số có tiệm cận ngang là \(n\leq m.\)
+ Nếu \(n=m\): tiệm cận ngang là đường thẳng \(y = \frac{a_n}{b_m}\)
+ Nếu \(n < m\) tiệm cận ngang là đường thẳng \(y=0.\)
2.2. Đường tiệm cận đứng
a) Định nghĩa
- Đường thẳng \(x=a\) được gọi là đường tiệm cận đứng của đồ thị hàm số \(y = f(x)\) nếu thỏa mãn một trong các điều kiện sau:
+ \(\lim_{x\rightarrow a^+} f(x) = \pm \infty\)
+ \(\lim_{x\rightarrow a^-} f(x) = \pm \infty\)
b) Chú ý
- Đường thẳng \(x=a\) là đường tiệm cận đứng của đồ thị \(y = f(x)\) thì a không thuộc tập xác định của \(f(x)\).
- Đối với hàm phân thức \(y = \frac{P(x)}{Q(x)}\) thì a là nghiệm Q(x)=0.