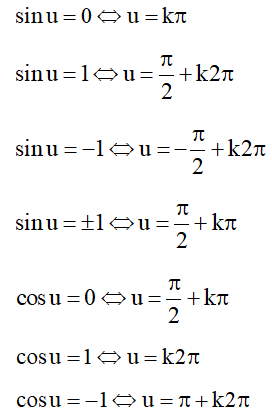1.1. Công thức lượng giác
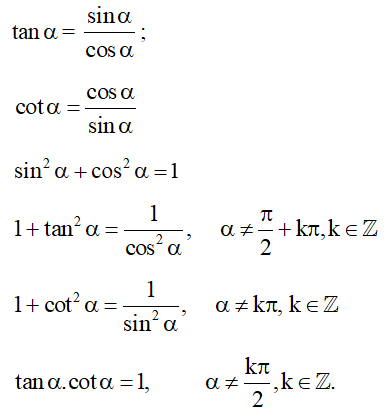
a. Công thức cộng
\(\begin{array}{l}
\sin (a + b) = \sin a\cos b + \cos a\sin b\\
\sin (a - b) = \sin a\cos b - \cos a\sin b\\
\cos (a + b) = \cos a\cos b - \sin a\sin b\\
\cos (a - b) = \cos a\cos b + \sin a\sin b\\
\tan (a + b) = \frac{{\tan a + \tan b}}{{1 - \tan a\tan b}}\\
\tan (a - b) = \frac{{\tan a - \tan b}}{{1 + \tan a\tan b}}
\end{array}\)
b. Công thức nhân đôi
\(\begin{array}{l}
\sin 2a = 2\sin a\cos a\\
\cos 2a = {\cos ^2}a - {\sin ^2}a\\
\tan 2a = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}
\end{array}\)
c. Công thức biến đổi tích thành tổng
\(\begin{array}{l}
\cos a\cos b = \frac{1}{2}[\cos (a + b) + \cos (a - b)]\\
\sin a\sin b = \frac{{ - 1}}{2}[\cos (a + b) - \cos (a - b)]\\
\sin a\cos b = \frac{1}{2}[\sin (a + b) + \sin (a - b)]
\end{array}\)
d. Công thức biến đổi tổng thành tích
\(\begin{array}{l}
\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\\
\cos u - \cos v = - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\\
\sin u + \sin v = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\\
\sin u - \sin v = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}
\end{array}\)
e. Công thức hạ bậc
\(\cos 2a = {\cos ^2}a - {\sin ^2}a = 2{\cos ^2}a - 1 = 1 - 2{\sin ^2}a\).
\({\cos ^2}a = \frac{{1 + \cos 2a}}{2};{\sin ^2}a = \frac{{1 - \cos 2a}}{2}\)
1.2. Gía trị lượng giác của các góc có liên quan đặc biệt
a. Hai góc đối nhau (\(\alpha \) và -\(\alpha \) )
\(\sin (-\alpha )=-\sin (\alpha )\)
\(\cos ( - \alpha ) = \cos (\alpha )\)
\(\tan ( - \alpha ) = - \tan (\alpha )\)
\(\cot ( - \alpha ) = - \cot (\alpha )\)
b. Hai góc hơn kém nhau (\(\alpha \) và \(\alpha +\pi \))
\(\sin (\alpha +\pi )=-\sin (\alpha )\)
\(\cos (\alpha + \pi ) = - \sin (\alpha )\)
\(\tan (\alpha + \pi ) = \tan (\alpha )\)
\(\cot (\alpha + \pi ) = \cot (\alpha )\)
c. Hai góc bù nhau (\(\alpha \) và \(\pi -\alpha \))
\(\sin (\pi -\alpha )=\sin (\alpha )\)
\(\cos (\pi -\alpha )=-\cos (\alpha )\)
\(\tan (\pi -\alpha )=-\tan (\alpha )\)
\(\cot (\pi -\alpha )=-\cot \alpha \)
d. Hai góc phụ nhau (\(\alpha \) và \(\frac{\pi }{2}-\alpha \))
\(\sin \left( \frac{\pi }{2}-\alpha \right)=\cos \alpha \)
\(\cos \left( {\frac{\pi }{2} - \alpha } \right) = \sin \alpha \)
\(\tan \left( {\frac{\pi }{2} - \alpha } \right) = \cot \alpha \)
\(\cot \left( {\frac{\pi }{2} - \alpha } \right) = \tan \alpha \)
1.3. Hàm số lượng giác
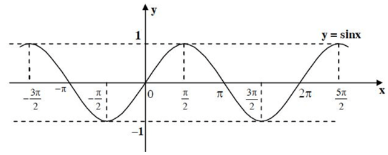
a. Hàm số sinx = m
- TXĐ : D = R và \( - 1 \le \sin x \le 1,\forall x \in R\).
- Là hàm số lẻ.
- Hàm số đồng biến trên \(\left( {\frac{{ - \pi }}{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\).
- Hàm số nghịch biến trên \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).
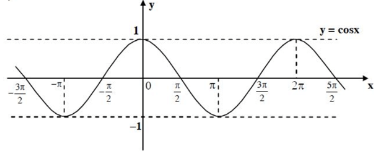
b. Hàm số cosx = m
- TXĐ : D = R và \( - 1 \le \cos x \le 1,\forall x \in R\).
- Là hàm số chẵn.
- Là hàm số có tuần hoàn chu kì π.
- Hàm số đồng biến trên \(\left( { - \pi + k2\pi ;k2\pi } \right)\).
- Hàm số nghịch biến trên \(\left( {k2\pi ;\pi + k2\pi } \right)\).
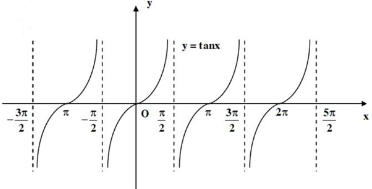
c. Hàm số tanx = m
- TXĐ : D = R.
- Là hàm số lẻ
- Là hàm số có tuần hoàn chu kì π.
- Hàm số đồng biến trên \(\left( {\frac{{ - \pi }}{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\).
- Có các đường tiệm cận \(x = \frac{\pi }{2} + k\pi \).
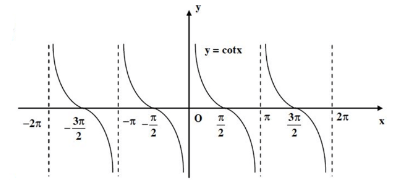
d. Hàm số cotx = m
- TXĐ : D = R \ \(\left\{ {k\pi , \in Z} \right\}\).
- Là hàm số lẻ
- Là hàm số có tuần hoàn chu kì π.
- Hàm số nghịch biến trên \(\left( {k\pi ;\pi + k\pi } \right)\).
- Có các đường tiệm cận \(x = k\pi \).
1.4. Phương trình lượng giác cơ bản
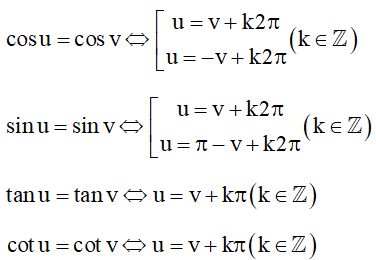
- Đặc biệt