Các tích nhận được từ sơ đồ hình cây của một tích các đa thức giống như cách lấy ra một đơn thức từ mỗi đa thức rồi nhân lại với nhau. Hơn nữa, tổng của chúng cho ta khai triển của tích các đa thức đã cho.
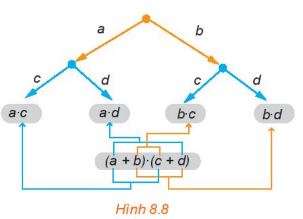
Chẳng hạn, trong sơ đỏ hình cây (H.8.8) của (a + b)(c + d) thì các tích nhận được là a.c, a.d, b.c, b.d cũng chính là các tích nhận được khi ta lấy một hạng tử của nhị thức thứ nhất (là a hoặc b) nhân với một hạng tử của nhị thức thứ hai (là c hoặc d). Ta có
\(\left( {a + b} \right).\left( {c + d} \right) = a.c + a.d + b.c + b.d\)
Ta có công thức sau:
| \(\begin{array}{l} {\left( {a + b} \right)^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}\\ \;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}. \end{array}\) |
|---|
Ví dụ: Khai triển \({\left( {2x + 1} \right)^4}\).
Giải
Thay a = 2x và b = 1 trong công thức khai triển của \({\left( {a + b} \right)^4}\), ta được:
\(\begin{array}{l}
{\left( {2x + 1} \right)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}.1 + 6.{\left( {2x} \right)^2}{.1^2} + 4.\left( {2x} \right){.1^3} + {1^4}\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = 16{x^4} + 32{x^3} + 24{x^2} + 8x + 1
\end{array}\)
Ta có công thức sau:
| \(\begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array}\) |
|---|
Ví dụ: Khai triển \({\left( {x + 3} \right)^5}\).
Giải
Thay a = x và b = 3 trong công thức khai triển của \({\left( {a + b} \right)^5}\), ta được:
\(\begin{array}{*{20}{l}}
{{{\left( {x + 3} \right)}^5} = {x^5} + 5.{x^4}.3 + 10.{x^3}{{.3}^2} + 10.{x^2}{{.3}^3} + 5.x{{.3}^4} + {3^5}}\\
{\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; = {x^5} + 15{x^4} + 90{x^3} + 270{x^2} + 405x + 243.}
\end{array}\)
Nhận xét: Các công thức khai triển \({\left( {a + b} \right)^n}\) với \(n \in \left\{ {4;5} \right\}\), là một công cụ hiệu quả để tính chính xác hoặc xấp xỉ một số đại lượng mà không cần dùng máy tính.