1.1. Khái niệm hàm số bậc hai
|
Hàm số bậc hai là hàm số cho bởi công thức \(y = a{x^2} + bx + c\) trong đó x là biến số, a, b, c là các hằng số và \(a \ne 0\). Tập xác định của hàm số bậc hai là R. |
|---|
Nhận xét
Hàm số \(y = a{x^2}(a \ne 0)\) đã học ở lớp 9 là một trường hợp đặc biệt của hàm số bậc hai với a = c = 0.
Ví dụ: Xét hàm số bậc hai y = -2x2 + 10x. Thay dấu "?" bằng các số thích hợp để hoàn thành bảng giá trị sau của hàm số.
Giải
Thay các giá trị của x vào công thức hàm số, ta được:
1.2. Đồ thị của hàm số bậc hai
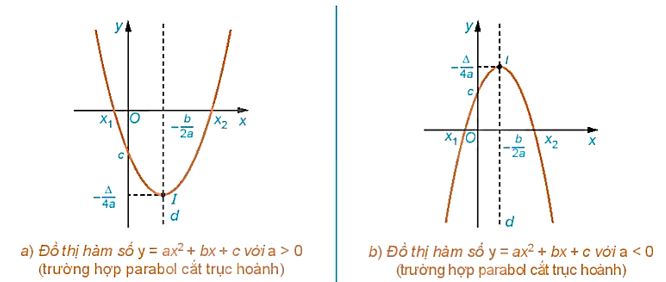
Gọi (P0) là Parabol y = ax2. nếu ta "dịch chuyển" (P0) theo vectơ \(\overrightarrow {OI} \) thì ta sẽ thu được đồ thị (P) của hàm số y = ax2 + bx + c có dạng như hình sau:
Nhận xét: Đồ thị hàm số y = ax2 + bx + c \(\left( {a \ne 0} \right)\) là một parabol.
|
+ Đồ thị hàm số y = ax2 + bx + c \(\left( {a \ne 0} \right)\) là một đường parabol có đỉnh là điểm \(I\left( { - \frac{b}{{2{\rm{a}}}}; - \frac{\Delta }{{4{\rm{a}}}}} \right)\) có trục đối xứng là đường thẳng \({x = - \frac{b}{{2{\rm{a}}}}}\). Parabol này quay bề lõm lên trên nếu a > 0, xuống dưới nếu a < 0. + Để vẽ đường parabol y = ax2 + bx + c ta tiến hành theo các bước sau: 1. Xác định toạ độ đính \(I\left( { - \frac{b}{{2{\rm{a}}}}; - \frac{\Delta }{{4{\rm{a}}}}} \right)\); 2. Vẽ trục đối xứng \({x = - \frac{b}{{2{\rm{a}}}}}\); 3. Xác định toạ độ các giao điểm của parabol với trục tung, trục hoành (nếu có) và một vài điểm đặc biệt trên parabol; 4. Vẽ parabol. |
|---|
Ví dụ: Vẽ parabol y = -2x2 - 2x + 4.
b) Từ đồ thị, hãy tìm khoảng đồng biến, nghịch biến và giá trị lớn nhất của hàm số y = -2x2 - 2x + 4..
Giải
a) Ta có a = -2 < 0 nên parabol quay bề lõm xuống dưới. Đỉnh \(I\left( { - \frac{1}{2};\frac{9}{2}} \right)\) Trục đối xứng \({x = - \frac{1}{2}}\). Giao điểm của đồ thị với trục Oy là A(0: 4). Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình y = -2x2 - 2x + 4, tức là x = 1 và x = -2.
Để vẽ đồ thị chinh xác hơn, ta có thể lấy thêm điểm đối xửng với A qua trục đối xứng \({x = - \frac{1}{2}}\) là \(B\left( { - 1;4} \right)\).
b) Từ đồ thị ta thầy:
+ Hàm số y = -2x2 - 2x + 4 đồng biến trên \(\left( { - \infty ; - \frac{1}{2}} \right)\) nghịch biến trên \(\left( { - \frac{1}{2}; + \infty } \right)\);
+ Giá trị lớn nhất của hàm số là \(y = \frac{9}{2}\), khi \(x = - \frac{1}{2}\).