1.1. Giá trị lượng giác của góc từ 0˚ đến 180˚
a) Giá trị lượng giác
|
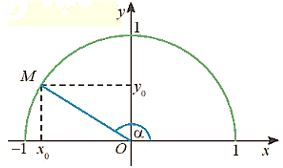
+) Với mỗi góc \(\alpha ({0^o} \le \alpha \le {180^o})\) có duy nhất điểm \(M({x_0};{y_0})\) trên nửa đường tròn đơn vị để \(\widehat {xOM} = \alpha .\) Khi đó: \(\sin \alpha = {y_0}\) là tung độ của M \(\cos \alpha = {x_0}\) là hoành độ của M \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }} = \frac{{{y_0}}}{{{x_0}}}(\alpha \ne {90^o})\) \(\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }} = \frac{{{x_0}}}{{{y_0}}}(\alpha \ne {0^o},\alpha \ne {180^o})\) |
|---|
Chú ý:
a) Nếu \(\alpha\) là góc nhọn thì các giá trị lượng giác của \(\alpha\) đều dương
Nếu ơ là góc tù thì sin\(\alpha\) > 0, cos\(\alpha\) < 0, tan\(\alpha\) < 0, cot\(\alpha\) < 0.
b) tan\(\alpha\) chỉ xác định khi \(\alpha \ne {90^0}\).
cot\(\alpha\) chỉ xác định khi \(\alpha \ne {0^0}\) và \(\alpha \ne {180^0}\).
b) Quan hệ giữa các giá trị lượng giác của hai góc bù nhau
Hai góc bù nhau, \(\alpha \) và \({180^o} - \alpha \):
| \(\begin{array}{l}\sin \left( {{{180}^o} - \alpha } \right) = \sin \alpha \\\cos \left( {{{180}^o} - \alpha } \right) = - \cos \alpha \\\tan \left( {{{180}^o} - \alpha } \right) = - \tan \alpha (\alpha \ne {90^o})\\\cot \left( {{{180}^o} - \alpha } \right) = - \cot \alpha ({0^o} < \alpha < {180^o})\end{array}\) |
|---|
Hai góc phụ nhau, \(\alpha \) và \({90^o} - \alpha \):
| \(\begin{array}{l}\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha \\\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha \\\tan \left( {{{90}^o} - \alpha } \right) = \cot \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\\\cot \left( {{{90}^o} - \alpha } \right) = \tan \alpha (\alpha \ne {90^o},{0^o} < \alpha < {180^o})\end{array}\) |
|---|
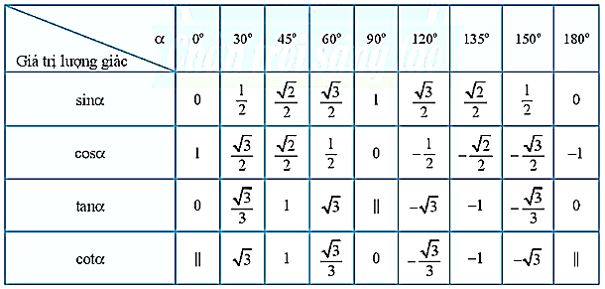
c) Giá trị lượng giác của một số góc đặc biệt
Chú ý: Trong bảng, kí hiệu "||" để chỉ giá trị lượng giác không xác định.
d) Sử dụng máy tính cầm tay để tính giá trị lượng giác của một góc
+ Tính các giá trị lượng giác của góc
Bước 1: Cài đặt đơn vị đo góc (độ hoặc radian)
Bước 2: Vào chế độ tính toán
Chú ý: Để tính \(\cot \alpha \) ta tính \(\frac{1}{{\tan \alpha }}\).
+ Xác định số đo của góc khi biết giá trị lượng giác của góc đó
Để tìm \(\alpha \) khi biết \(\cot \alpha \) ta tính \(\tan \alpha = \frac{1}{{\cot \alpha }}\) rồi tính \(\alpha \) sau.
1.2. Định lí cosin và định lí sin
a) Định lí cosin trong tam giác
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - 2bc\cos A\\{b^2} = {c^2} + {a^2} - 2ca\cos B\\{c^2} = {a^2} + {b^2} - 2ab\cos C\end{array}\)
Hệ quả
\(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}};\cos C = \frac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\)
b) Định lí sin trong tam giác
Trong tam giác ABC với BC = a, CA = b, AB = c, ta có:
\(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R.\)
(R là bán kính đường tròn ngoại tiếp tam giác ABC)
Hệ quả
\(a = 2R.\sin A;\quad b = 2R\sin B;\quad c = 2R\sin C\)
\(\sin A = \frac{a}{{2R}};\quad \sin B = \frac{b}{{2R}};\quad \sin C = \frac{c}{{2R}}.\)
c) Các công thức tính diện tích tam giác
1) \(S = \frac{1}{2}a{h_a} = \frac{1}{2}b{h_b} = \frac{1}{2}c{h_c}\)
2) \(S = \frac{1}{2}bc\sin A = \frac{1}{2}ca\sin B = \frac{1}{2}ab\sin C\)
3) \(S = \frac{{abc}}{{4R}}\)
4) \(S = pr = \frac{{(a + b + c).r}}{2}\)
5) \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (Công thức Heron)