1.1. Định lí về dấu của tam thức bậc hai
|
Cho tam thức bậc hai \(f(x) = a{x^2} + bx + c\) với \(a \ne 0,\Delta = {b^2} - 4ac.\) + \(\Delta < 0\): f(x) cùng dấu với a, \(\forall x \in \mathbb{R}\) + \(\Delta = 0\): f(x) cùng dấu với a, \(\forall x \in \mathbb{R}{\rm{\backslash }}\left\{ {\frac{{ - b}}{{2a}}} \right\}\) + \(\Delta > 0\): f(x) có 2 nghiệm \({x_1},{x_2}({x_1} < {x_2})\), khi đó f(x) cùng dấu với hệ số a với mọi x thuộc các khoảng \(\left( { - \infty ;{x_1}} \right)\) và \(\left( {{x_2}; + \infty } \right)\); f(x) trái dấu với hệ số a với mọi x thuộc khoảng \(\left( {{x_1};{x_2}} \right)\). |
|---|
Nhận xét: Trong định lí, có thể thay biệt thức \(\Delta = {b^2} - 4{\rm{a}}c\) bằng biệt thức thu gọn \(\Delta ' = {\left( {b'} \right)^2} - {\rm{a}}c\) với b = 2b'
1.2. Ví dụ
Ví dụ 1: Xét dấu của tam thức bậc hai: \(f(x) = 2{x^2} + 3x - 2\)
Giải
\(\Delta = {3^2} - 4.2.( - 2) = 25 > 0\)
Tam thức bậc hai \(f(x) = 2{x^2} + 3x - 2\) có hai nghiệm phân biệt \({x_1} = - 2,{x_2} = \frac{1}{2}\) và hệ số \(a = 2 > 0\)
Ta có bảng xét dấu \(f(x)\) như sau:
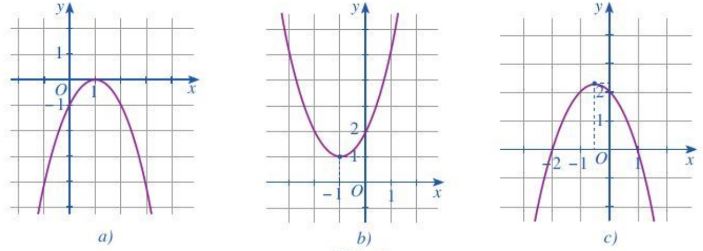
Ví dụ 2: Tìm nghiệm và lập bảng xét dấu của tam thức bậc hai f(x) ứng với đô thị hàm số y = f(x) được cho ở mỗi hình sau.
Giải
a) Từ đỗ thị Hình a ta có nghiệm của tam thức bậc hai f(x) là x = 1. Bảng xét dấu tam thức f(x) là:
b) Từ đồ thị Hình b ta có tam thức bậc hai f(x) vô nghiệm. Bảng xét dấu tam thức f(x) là:
c) Từ đồ thị Hình c ta có tam thức bậc hai f(x) có hai ngghiệm là x1 = -2 và x2 = 1. Bảng xét dấu tam thức f(x) là: