2.1.1. Thí nghiệm giao thoa sóng mặt nước

– Gắn hai hòn bi nhỏ vào thanh đàn hồi P và cho chúng chạm mặt nước.

– Khi thanh dao động, hai hòn bi ở A và B tạo ra trên mặt nước hai hệ sóng lan truyền theo những hình tròn đồng tâm mở rộng dần và đan trộn vào nhau.

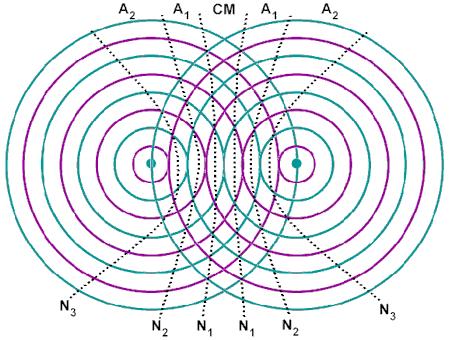
– Khi hình ảnh sóng đã ổn định, trên mặt nước có hai nhóm đường cong cố định: một nhóm có biên độ dao động cực đại xen kẽ với một nhóm khác tại đó mặt nước không dao động (biên độ cực tiểu).

– Hiện tượng trên gọi là hiện tượng giao thoa của sóng nước.

2.1.2. Nguồn kết hợp – sóng kết hợp

– Nguồn kết hợp: Là hai nguồn dao động cùng phương, cùng tần số, cùng pha hoặc có độ lệch pha không đổi theo thời gian (Δφ = const).

– Sóng kết hợp: Là hai sóng được tạo ra từ hai nguồn kết hợp.

– Trên mặt nước có sự lan truyền của hai sóng kết hợp và tại các điểm có sự gặp nhau của hai sóng kết hợp, ta có sự tổng hợp hai sóng.

2.1.3. Điều kiện để có giao thoa

– Điều kiện xảy ra giao thoa là 2 sóng kết hợp gặp nhau và dao động cùng phương.

– Hai sóng phải là sóng kết hơp: Tức là cùng tần số và có độ lệch pha không đổi theo thời gian.

2.2.1. Các phương trình sóng do nguồn A và nguồn B truyền tới điểm M

– Xét điểm M cách A và B các đoạn \(d_1; d_2\) (AB << \(d_1; d_2\)  để có thể coi biên độ các sóng truyền tới M là bằng nhau). Sóng từ A và B truyền đến M với vận tốc v.

– Giả sử 2 sóng A và B có cùng phương trình dao động là: \(\small u_A=u_B= a cos \omega t\)

+ Điểm M cách nguồn A đoạn \(d_1\) , cách nguồn B đoạn \(d_2\) . 

+ Phương trình dao động tại M do sóng A truyền đến là:  \(u_{1M}=acos(\omega t-2\pi \frac{d_1}{\lambda })\)

+ Phương trình dao động tại M do sóng B truyền đến là: \(u_{2M}=acos(\omega t-2\pi \frac{d_2}{\lambda })\)

2.2.2. Độ lệch pha giữa hai sóng kết hợp

 

 \(\Delta \varphi =\left |(-2\pi \frac{d_2}{\lambda })- (-2\pi \frac{d_1}{\lambda }) \right | =\frac{2\pi }{\lambda }\left | d_1-d_2 \right |\)

⇔ \(\Delta \varphi =\frac{2\pi }{\lambda }\left | d_1-d_2 \right |\)

Trong đó : 

 \(d=\left | d_1-d_2 \right |\) là hiệu đường đi của 2 sóng từ 2 nguồn đến điểm đang xét trong vùng giao thoa (m)

\(\small \lambda\): Bước sóng (m)

\(\small \Delta \varphi\) : Độ lệch pha của 2 sóng 

2.2.3. Phương trình dao động tổng hợp

\(u_M=u_{1M}+u_{2M}=acos(\omega t-2\pi \frac{d_1}{\lambda })+ acos(\omega t-2\pi \frac{d_2}{\lambda }) =Acos(\omega t+\varphi )\)

– Biên độ tổng hợp:  \(A_M=2a.\left | cos[\frac{\pi}{\lambda }.(d_2-d_1)] \right |\)

– Độ lệch pha của 2 sóng tại M: \(\Delta \varphi _M=\frac{2\pi}{\lambda }.(d_2-d_1)\)

– Pha ban đầu của sóng tại M:
\(\varphi _M=\varphi -\frac{\pi}{\lambda }.(d_1+d_2)\)

2.3.1. Dao động của một điểm trong vùng giao thoa:

– Cho 2 nguồn \(S_1\) và \(S_2\) có cùng f , cùng pha

– Phương trình dao động tại 2 nguồn: 

\(u_1 =u_2=Acos\omega t=Acos\frac{2\pi t}{T}\)

– Xét điểm M cách \(S_1\) và \(S_2\)  một đoạn :

d1 = \(S_1\)M và   d2 = \(S_2\)M 

– Coi biên độ bằng nhau và không đổi trong quá trình truyền sóng .

– Phương trình sóng từ  

\(S_1\) đến M :\(u_{1M} =Acos\frac{2\pi }{T}(t-\frac{d_1}{v})=Acos2\pi (\frac{t}{T}-\frac{d_1}{\lambda })\)

– Phương trình sóng từ

\(S_2\) đến M :\(u_{2M} =Acos\frac{2\pi }{T}(t-\frac{d_2}{v})=Acos2\pi (\frac{t}{T}-\frac{d_2}{\lambda })\)

– Phương trình Sóng tổng hợp tại M :

\(u_M=u_{1M}+u_{1M}=A.\left [cos2\pi (\frac{t}{T}-\frac{d_1}{\lambda })+cos2\pi (\frac{t}{T}-\frac{d_2}{\lambda }) \right ]\)

\(u_M=2A.cos\frac{\pi -(d_1-d_2)}{\lambda }.cos2\pi (\frac{t}{T}-\frac{(d_1+d_2)}{\lambda })\)

– Biên độ dao động là :  

\(A=2A.\left | cos\frac{\pi (d_2-d_1)}{\lambda } \right |\) 

2.3.2. Vị trí cực đại và cực tiểu giao thoa

– Vị trí các cực đại giao thoa

\((A_M)_{max}=2a\Leftrightarrow cos[\frac{\pi}{\lambda }(d_2-d_1)]=\pm 1\)
\(\Rightarrow \frac{\pi}{\lambda }(d_2-d_1)=k\pi\Rightarrow d_2-d_1=k\lambda , k\in Z\)
\(k=0\Rightarrow d_2-d_1=0\) đường cực đại trung tâm.
\(k=\pm 1\Rightarrow d_2-d_1=\pm .\lambda\) đường cực đại bậc 1.
\(k=\pm 2\Rightarrow d_2-d_1=\pm 2\lambda\) đường cực đại bậc 2.

– Ví trí các cực tiểu giao thoa :

\((A_M)_{min}=0\Leftrightarrow cos[\frac{\pi}{\lambda }(d_2-d_1)]=0\)
\(\Rightarrow \frac{\pi}{\lambda }(d_2-d_1)=(k+\frac{1}{2})\pi\)
\(\Rightarrow d_2-d_1=(k’+\frac{1}{2})\lambda =(2k’+1)\frac{\lambda }{2},k’\in Z\)
\(\bigg \lbrack\begin{matrix} k’=0\Rightarrow d_2-d_1=\frac{1}{2}\lambda \\ k’=-1\Rightarrow d_2-d_1=-\frac{1}{2}\lambda \end{matrix}\) đường cực tiểu thứ 1
\(\bigg \lbrack\begin{matrix} k’=1\Rightarrow d_2-d_1=\frac{3}{2}\lambda \\ k’=-2\Rightarrow d_2-d_1=-\frac{3}{2}\lambda \end{matrix}\)  đường cực tiểu thứ2

– Tóm lại:

 \(\frac{\left | d_2-d_1 \right |}{\lambda }=\left\{\begin{matrix} k\Rightarrow M \ thuoc \ cuc \ dai \ bac \ k\\ k+\frac{1}{2}\Rightarrow M \ thuoc \ cuc \ tieu \ bac \ (k+1) \end{matrix}\right.\)

– Suy ra :

+ Hiệu đường đi = một số nửa nguyên lần bước sóng

+ Quỹ tích các điểm này là những đường Hypebol có 2 tiêu điểm là  \(S_1\) và \(S_2\) gọi là những vân giao thoa cực tiểu.

– Giao thoa sóng là sự gặp nhau của hai hay nhiều sóng kết hợp trong không gian, trong đó có những điểm cố định mà tại đó biên độ sóng được tăng cường hay giảm bớt.