– Ta có thể biểu diễn một dao động  \(x = A\cos (\omega t + \varphi )\) bằng một vectơ   quay \(\overrightarrow{OM}\)  tại  thời điểm ban đầu có các đặc điểm sau:

+ Có góc tai góc tọa độ của Ox

+ Có độ dài bằng biên độ dao động; OM = A.

+ Hợp với Ox một góc \(\small \varphi\)

– Hay:  \(\overrightarrow{OM} \left\{\begin{matrix} |\overrightarrow{OM}| = A \ \ \ \ \\ (\overrightarrow{OM},\Delta ) = \varphi \end{matrix}\right.\)

a. Đặt vấn đề

– Tìm tổng của hai dao động

\(\left\{\begin{matrix} x_1 = A_1 \cos (\omega t + \varphi _1)\\ x_2 = A_2 \cos (\omega t + \varphi _2) \end{matrix}\right.\)

b. Phương pháp giản đồ Fre-nen

– Ta lần lượt ta vẽ hai vec tơ quay đặt trưng cho hai dao động:

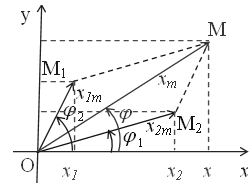
– Ta thấy \(\small \underset{OM_1}{\rightarrow}\) và \(\small \underset{OM_2}{\rightarrow}\) quay với tốc độ góc ω thì \(\small \underset{OM}{\rightarrow}\) cũng quay với tốc độ góc là ω.

– Phương trình tổng hợp

    \(x = A\cos (\omega t + \varphi )\)

\(\small \Rightarrow\) Kết luận: Dao động tổng hợp của hai dao động điều hòa cùng phương, cùng tần số là một dao động điều hòa cùng phương, cùng tần số với hai dao động đó.

– Trong đó:

\(A = \sqrt{A_{1}^{2} + A_{2}^{2} + 2A_1A_2\cos (\varphi _2 – \varphi _1)}\)  (1)

\(\tan \varphi = \frac{A_1 \sin \varphi _1 + A_2 \sin \varphi _2}{A_1 \cos \varphi _1 + A_2 \cos \varphi _2}\)      (2)

c.  Ảnh hưởng của độ lệch  pha

\(\ \Delta \varphi = \varphi _2 – \varphi _1 = k2 \pi\): x₁, x₂ cùng pha \(\Rightarrow \left\{\begin{matrix} A = A_1 + A_2\\ \varphi = \varphi _1 = \varphi _2 \end{matrix}\right.\)

\(\ \Delta \varphi = \varphi _2 – \varphi _1 = (2k + 1) \pi\): x₁, x₂ ngược pha \(\Rightarrow \left\{\begin{matrix} A = |A_1 – A_2| \ \ \ \ \ \ \ \ \\ \varphi = \varphi _1 \ neu\ A_1 > A_2 \end{matrix}\right.\)

\(\ \Delta \varphi = (2k + 1) \frac{\pi}{2} \Rightarrow x_1 \perp x_2 \Rightarrow A = \sqrt{A_{1}^{2} + A_{2}^{2}}\)