1.1. Chuyển động thẳng
– Chuyển động thẳng là chuyển động thường gặp trong đời sống, có quỹ đạo chuyển động là đường thẳng.
– Khi vật chuyển động thẳng theo một chiều không đổi thì độ dịch chuyển và quãng đường đi được có độ lớn như nhau d= s; vận tốc và tốc độ có độ lớn như nhau V = v.
– Khi vật đang chuyển động thẳng theo chiều dương, nếu đổi chiều chuyển động thì trong khoảng thời gian chuyển động ngược chiều đó quãng đường đi được vẫn có giá trị dương, còn độ dịch chuyển có giá trị âm; tốc độ vẫn có giá trị dương còn vận tốc có giá trị âm V= -v.
– Dựa vào các công thức v = s/t và \(\overrightarrow v = \frac{{\overrightarrow d }}{t}\) ta có thể xác định được quãng đường đi được, độ dịch chuyển, tốc độ và vận tốc của chuyển động.
1.2. Đồ thị độ dịch chuyển – Thời gian trong chuyển động thẳng
Đồ thị độ dịch chuyển – thời gian của một chuyển động không những cho phép mô tả được chuyển động, mà còn có thể cho biết nhiều thông tin khác nữa về chuyển động.
a. Cách vẽ đồ thị độ dịch chuyển – thời gian (d-t) trong chuyển động thẳng đều
– Đồ thị đơn giản nhất là đồ thị độ dịch chuyển – thời gian của chuyển động thẳng đều.
– Trong chuyển động thẳng đều thì d= vt (với v là một hằng số).
– Biểu thức d = v.t có dạng giống biểu thức của hàm số y = ax đã học trong môn Toán nên có đường biểu diễn là một đoạn thẳng.
b. Sử dụng đồ thị độ dịch chuyển – thời gian trong chuyển động thẳng
– Đồ thị của các hàm số đã học trong môn Toán
+ y = a,x (a > 0)
+ y = ax + b ( a < 0, b > 0)
→ Khi vật chuyển động thẳng với vận tốc không đổi v > 0 thì d = vt. Phương trình này có dạng hàm số y = ax
→ Khi vật đang chuyển động thẳng, theo chiều dương, nếu đổi chiều chuyển động thì trong khoảng thời gian chuyển động ngược chiều đó, quãng đường đi được vẫn có giá trị dương còn độ dịch chuyển có giá trị âm. Đồ thị độ dịch chuyển – thời gian có dạng như y = ax + b
1.3. Vận tốc và đồ thị độ dịch chuyển – thời gian trong chuyển động thẳng
Từ đồ thị độ dịch chuyển – thời gian có thể dễ dàng tính được giá trị của vận tốc.
Trong đồ thị vẽ ở hình dưới đây, hệ số góc (độ dốc) của đường biểu diễn 0A là:
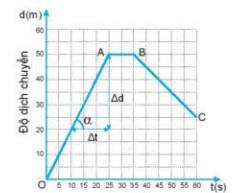
\(\frac{{\Delta d}}{{\Delta t}} = \frac{{50 – 20}}{{25 – 10}} = \frac{{30}}{{15}} = 2m/s\)
Đây chính là độ lớn vận tốc của người bơi trong 50 m đầu y = 2 m/s.
Độ dốc của đồ thị độ dịch chuyển- thời gian trong chuyển động thẳng cho biết vận tốc chuyển động.