– Khi vật chuyển động thì vị trí của vật so với vật được chọn làm mốc thay đổi theo thời gian. Bài toán cơ bản của động học là xác định vị trí của vật tại các thời điểm khác nhau.

– Để xác định vị trí của vật, người ta dùng hệ toạ độ có gốc là vị trí của vật mốc, trục hoành Ox và trục tung ly. Các giá trị trên các trục toạ độ được xác định theo một tỉ lệ xác định.

Ví dụ, nếu tỉ lệ là 1/1000 thì vị trí của điểm A trong Hình 4.1 được xác định trên hệ toạ độ là A (x = 10 m; y= 20 m) và của điểm B là B(x = – 10 m; y = 20 m).

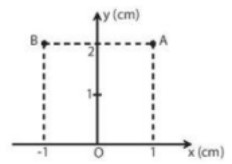
Tỉ xich 1 cm ứng với 10 m

Hình 4.1. Hệ toạ độ

– Động học là phần vật lí nghiên cứu chuyển động của vật mà không đề cập đến tác dụng của lực lên chuyển động.

– Khi kích thước của vật rất nhỏ so với độ dài của quãng đường đi được thì vật được coi là chất điểm. Trong chương này chúng ta chỉ tìm hiểu chuyển động của chất điểm.

– Trong thực tế, người ta thường chọn hệ toạ độ trùng với hệ toạ độ địa lí, có gốc là vị trí của vật mốc, trục hoành là đường nối hai hướng địa lí Tây – Đông, trục tung là đường nối hai hướng địa lí Bắc – Nam (Hình 4.2).

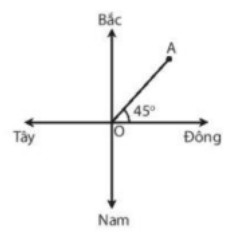
Hình 4.2. Hệ toạ độ địa lí

Ví dụ nếu 0A = 2 cm và tỉ lệ là 1/1000 thì vị trí của điểm A cách điểm gốc 20 m theo hướng 45° Đông – Bắc:

A (d = 20 m; 45° Đông – Bắc).

– Để xác định thời điểm, người ta phải chọn một gốc thời gian, đo khoảng cách Biết vật thời điểm cần xác định.

Ví dụ nếu chọn gốc thời gian là t_o = 8 h và thời gian chuyển động là \(\Delta t\) = 2 h, thì thời điểm khi kết thúc chuyển động là t = t_o + \(\Delta t\) = 10 h.

– Hệ toạ độ kết hợp với mốc thời gian và đồng hồ đo thời gian được gọi là hệ quy chiếu.

Chú ý: Khi vật chuyển động trên đường thẳng thì chỉ cần dùng hệ toạ độ có điểm gốc 0 (vị trí của vật mốc) và trục Ox trùng với quỹ đạo chuyển động của vật. Ở

– Trong bài toán ở phần mở bài, biết quãng đường đi được có thể xác định được khoảng cách giữa điểm đầu và điểm cuối của chuyển động, nhưng chưa đủ để xác định vị trí của vật.

– Muốn xác định được vị trí của vật phải biết thêm hướng của chuyển động. Ví dụ, nếu biết ô tô chuyển động theo hướng Bắc thì dễ dàng xác định được vị trí của ô tô là điểm B trên bản đồ.

– Đại lượng vừa cho biết độ dài vừa cho biết hướng của sự thay đổi vị trí của vật gọi là độ dịch chuyển. Độ dịch chuyển của ô tô trong bài toán trên là: d_OB = 100 m (Bắc)

Một đại lượng vừa cho biết độ lớn, vừa cho biết hướng như độ dịch chuyển gọi là đại lượng vectơ.

Độ dịch chuyển được biểu diễn bằng một mũi tên nổi vị trí đầu và vị trí cuối của chuyển động, có độ dài tỉ lệ với độ lớn của độ dịch chuyển. Kí hiệu là \(\overrightarrow d \)

Ví dụ dưới đây giúp chúng ta phân biệt độ dịch chuyển và quãng đường đi được.

Trong Hình 4.3 người đi xe máy (1), người đi bộ (2), người đi ô tô (3) đều khởi hành từ siêu thị A để đi đến bưu điện B.

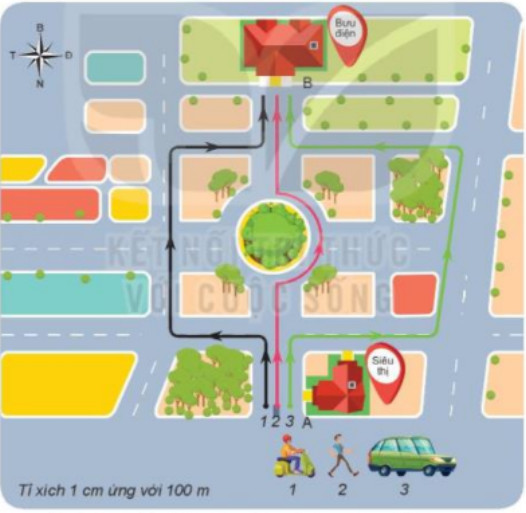
Hình 4.3. Sơ đồ mô tả quãng đưỏng đi được của người đi xe máy,

Có thể dùng phép cộng vectơ để tổng hợp độ dịch chuyển của vật.

Bài tập ví dụ: Hai người đi xe đạp từ A đến C, người thứ nhất đi theo đường từ A đến B, rồi từ B đến C; người thứ hai đi thẳng từ A đến C (Hình 4.4). Cả hai đều về đích cùng một lúc.

Hãy tính quãng đường đi được và độ dịch chuyển của người thứ nhất và người thứ hai. So sánh và nhận xét kết quả.

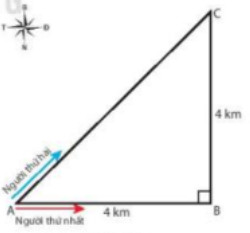
Hình 4.4

Giải

Quãng đường đi được của người thứ nhất:

S₁ = AB + BC = 4 + 4 = 8 km

Vì ABC là tam giác vuông nên độ lớn của độ dịch chuyển \(\overrightarrow {AC} \) của người thứ nhất được tính bằng công thức:

\({d_1} = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{4^2} + {4^2}}  \approx 5,7km\)

Vì ABC là tam giác vuông cân nên \(\widehat {CAB}\) = 45°. Hướng của độ dịch chuyển là hướng 45° Đông – Bắc.

Độ dịch chuyển của người thứ nhất là: d₁ = 5,7 km (hướng 45° Đông – Bắc).

Quãng đường đi được của người thứ hai là:

S₂ = AC = 5,7 km

Độ dịch chuyển của người thứ hai là:

d₂ = 5,7 km, hướng 45° Đông – Bắc

Bảng 4.2

	Người thứ nhất	Người thứ hai
Quãng đường đi được	s1 = 8 km	s2 = 5,7 km
Độ dịch chuyển	d1 = 5,7 km	d2 = 5,7 km

Dựa vào kết quả ở Bảng 4.2, ta thấy:

– Vì sự dịch chuyển vị trí của người thứ nhất và người thứ hai là như nhau đều từ A đến C, nên hai người có cùng độ dịch chuyển.

– Tuy về đích cùng một lúc nhưng người thứ nhất đi nhanh hơn vì phải đi quãng đường dài hơn. Tuy nhiên nếu chỉ chú ý đến sự thay đổi vị trí thì phải coi cả hai đều thay đổi vị trí nhanh như nhau.