a. Hệ kín (hay hệ cô lập)

– Một hệ nhiều vật được gọi là hệ kín khi không có ngoại lực tác dụng lên hệ hoặc nếu có thì các lực ấy cân bằng nhau. Trong một hệ kín, chỉ có các nội lực (các lực tác dụng giữa các vật trong hệ) tương tác giữa các vật. Các nội lực này theo định luật 3 Newton thực đối nhau từng đổi một.

b. Định luật bảo toàn động lượng

– Xét một hệ kín gồm hai vật trượt trên một đệm khí đến va chạm với nhau. Vì các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là cặp nội lực trực đối nhau, nên theo định luật III Newton, ta viết:

\(\overrightarrow {{F_1}} \) = – \(\overrightarrow {{F_2}} \)            (29.1)

– Dưới tác dụng của các lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \), trong khoảng thời gian \(\Delta t\), động lượng của mỗi vật có độ biến thiên lần lượt là \(\Delta \overrightarrow {{p_1}} \) và \(\Delta \overrightarrow {{p_2}} \)

– Áp dụng công thức \(\overrightarrow {{F}} \Delta t = \Delta \overrightarrow p \) cho từng vật, ta có:

\(\left\{ \begin{array}{l}
\overrightarrow {{F_1}} \Delta t = \Delta \overrightarrow {{p_1}} \\
\overrightarrow {{F_2}} \Delta t = \Delta \overrightarrow {{p_2}} 
\end{array} \right.\)    (29.2)

– Từ (29.1) và (29.2), suy ra:

\(\Delta \overrightarrow {{p_1}}  =  – \Delta \overrightarrow {{p_2}} \) hay \(\Delta \overrightarrow {{p_1}}  + \Delta \overrightarrow {{p_2}}  = \overrightarrow 0 \)

– Gọi \(\Delta \overrightarrow {{p_1}}  + \Delta \overrightarrow {{p_2}}  = \overrightarrow 0 \) là động lượng toàn phần của hệ. Ta có biến thiên động lượng toàn phần của hệ bằng tổng các biến thiên động lượng của mỗi vật: \(\Delta \overrightarrow p  = \Delta \overrightarrow {{p_1}}  + \Delta \overrightarrow {{p_2}}  = \overrightarrow 0 \)

– Biến thiên động lượng của hệ bằng không, nghĩa là động lượng toàn phần của hệ không đổi.

\(\overrightarrow p  = {\overrightarrow p _1} + {\overrightarrow p _2}\) = không đổi

– Kết quả này có thể mở rộng cho hệ kín gồm nhiều vật.

– Từ đó, ta có thể phát biểu: Động lượng toàn phần của hệ kín là một đại lượng bảo toàn.

– Phát biểu trên được gọi là định luật bảo toàn động lượng.

– Định luật bảo toàn động lượng có nhiều ứng dụng thực tế: giải các bài toán va chạm, làm cơ sở cho nguyên tắc chuyển động phản lực.

– Một hệ nhiều vật tác dụng lẫn nhau được gọi là hệ kín (hay hệ cô lập) khi không có ngoại lực tác dụng vào hệ hoặc khi các ngoại lực cân bằng nhau. – Định luật bảo toàn động lượng: “Động lượng toàn phần của hệ kín là một đại lượng bảo toàn”.

Có hai kiểu va chạm thường gặp là va chạm đàn hồi và va chạm mềm.

a. Va chạm đàn hồi

Hình 29.1 mô tả một thí nghiệm về va chạm đàn hồi.

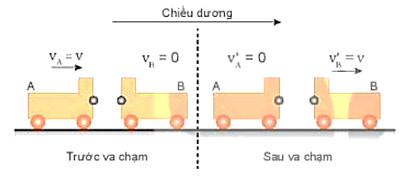
Hình 29.1. Va chạm đàn hồi

– Dùng hai xe A và B giống nhau, ở đầu mỗi xe có gắn một quả cầu kim loại nhỏ, cho xe A chuyển động với vận tốc v_A = v tới va chạm với xe Bđang đứng yên. Kết quả của va chạm làm xe A đang chuyển động thì dừng lại, còn xe B đang đứng yên thì chuyển động với đúng vận tốc V’_B = v.

– Va chạm như thế gọi là va chạm đàn hồi.

b. Va chạm mềm

– Hình 29.2 mô tả một thí nghiệm về va chạm mềm.

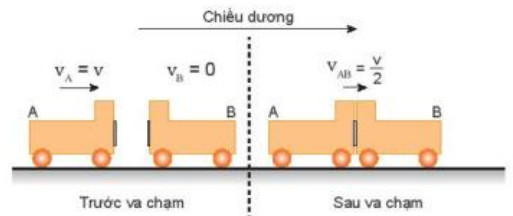
Hình 29.2. Va chạm mềm

– Dùng hai xe A và B giống nhau, ở đầu mỗi xe có gắn một miếng nhựa dính. Cho xe A chuyển động với vận tốc v_A = v tới va chạm với xe kia đang đứng yên. Sau va chạm, cả hai xe dính vào nhau và chuyển động với vận tốc bằng V_AB = v/2. Kiểu va chạm “dính” này gọi là va chạm mềm.

Có hai kiểu va chạm thường gặp là va chạm đàn hồi và va chạm mềm.