Vật Lý 10 Chân trời sáng tạo Bài 3: Đơn vị và sai số trong Vật Lý

1.1. Đơn vị và thứ nguyên trong Vật lý

a. Hệ đơn vị SI, đơn vị cơ bản và đơn vị dẫn xuất

– Trong chương trình môn Khoa học tự nhiên ở Trung học Cơ sở, các em đã tìm hiểu một số đại lượng vật lí như: khối lượng, chiều dài, thời gian, diện tích, thể tích, áp suất, nhiệt độ,… và cũng đã thực hành đo từ lớp 6. Kết quả của phép đo bao gồm hai thông tin: số do cho biết giá trị của đại lượng đang xét và đơn vị của số đo.

– Tập hợp của đơn vị được gọi là hệ đơn vị. Trong khoa học Có rất nhiều hệ đơn vị được sử dụng, trong đó thông dụng nhất là hệ đơn vị đo lường quốc tế SI (Système International dunités) được xây dựng trên cơ sở của 7 đơn vị cơ bản (Bảng 3.1).

Bảng 3.1. Các đơn vị cơ bản trong hệ SI

STT	Đơn vị	Kí hiệu	Đại lượng
1	mét	m	Chiều dài
2	kilogam	kg	Khối lượng
3	giây	s	Thời gian
4	kelvin	K	Nhiệt độ
5	ampe	A	Cường độ dòng điện
6	mol	mod	Lượng chất
7	candela	cd	Cường độ ánh sáng

– Khi số đo của đại lượng đang xem xét là một bội số hoặc ước số thập phân của mười, ta có thể sử dụng tiếp đâu ngữ như trong Bảng 3.2 ngay trước đơn vị để phần số đo được trình bày ngắn gọn.

Bảng 3.2. Tên và kí hiệu tiếp đấu ngữ của

Kí hiệu	Tên đọc	Hệ số	Kí hiệu	Tên đọc	Hệ số
Y	yotta	1024	y	yokto	10^–24
Z	zetta	10²¹	z	zepto	10–21
E	eta	1028	a	atto	10–18
P	peta	1015	f	femto	10–15
T	tera	1012	P	pico	10–12
G	giga	109	n	nano	10–9
M	mega	106	\(\mu \)	micro	10–6
k	kilo	103	m	mili	10–3
h	hecto	102	c	centi	10–2
da	deka	101	d	deci	10-1

Ví dụ: Ta có thể viết quãng đường từ Thành phố Hồ Chí Minh đến Thủ đô Hà Nội là khoảng 1730 km thay vì 1730.10³ m, hoặc khối lượng trung bình của một con muỗi có thể được viết là 2 mg thay vì 2-10^-3g.

– Ngoài 7 đơn vị cơ bản, những đơn vị còn lại được gọi là đơn vị dẫn xuất. Mọi đơn vị dẫn xuất đều có thể phân tích thành các đơn vị cơ bản dựa vào mối liên hệ giữa các đại lượng tương ứng.

b. Thứ nguyên

– Thử nguyên của một đại lượng là quy luật nêu lên sự phụ thuộc của đơn vị đo đại lượng đó vào các đơn vị cơ bản.

– Thứ nguyên của một đại lượng X được biên diễn dưới dạng [X]. Thứ nguyên của một số đại lượng cơ bản thường sử dụng được thể hiện trong Bảng 3.3.

Bảng 3.3. Thứ nguyên của một số đại lượng cơ bản

Đại lượng cơ bản	Thứ nguyên
[Chiều dài]	L
[Khối lượng]	M
[Thời gian]	T
[Cường độ dòng điện]	I
[Nhiệt độ]	K

Một đại lượng vật lí có thể được biểu diễn bằng nhiều đơn vị khác nhau nhưng chỉ có một thử nguyên duy nhất. Một số đại lượng vật lí có thể có cùng thứ nguyên.

Ví dụ:

– Toạ độ, quãng đường đi được có thể được biểu diễn bằng đơn vị mét, cây số, hải lý, feet, dặm,… nhưng chỉ có một thứ nguyên L.

– Tốc độ, vận tốc có thể được biểu diễn bằng đơn vị m/s, km/h, dặm/giờ nhưng chỉ có một thứ nguyền L.T^-1.

Lưu ý: Trong các biểu thức vật lí:

– Các số hạng trong phép cộng (hoặc trừ) phải có cùng thứ nguyên.

– Hai vế của một biểu thức vật lí phải có cùng thử nguyên.

c. Vận dụng mối liên hệ giữa đơn vị dẫn xuất với 7 đơn vị cơ bản của hệ SI

Ví dụ: Để xác định quãng đường đi được s của một chất điểm chuyển động thẳng đều, một bạn học sinh đã viết thời gian như sau: s = \(\alpha \).v.t² với v và t lần lượt là vận tốc và thời gian, \(\alpha \) là hằng số không thử nguyên. Dựa vào việc xác định thử nguyên, em hãy cho biết công thức trên là đúng hay sai.

Bài giải

– Thử nguyên của các đại lượng s, v và t lần lượt là L, L.T^-1 và T.

– Từ đó, ta thấy vế trái của công thức trên có thứ nguyên L trong khi vế phải lại có thứ nguyên L.T.

– Do 2 vế của công thức không cùng thử nguyên nên bạn học sinh chưa đưa ra được Công thức chính xác.

– Dựa vào phân tích thử nguyên, ta cần sửa lại công thức chính xác như sau: s = \(\alpha \).v.t

– Trong hệ SI, s, v và t lần lượt có đơn vị là m, m.s^-1, s.

1.2. Sai số trong phép đo và cách hạn chế

a. Các phép đo trong Vật lí

Hình 3.1. a) Bình chia độ b) Cân

– Phép đo các đại lượng vật lí là phép so sánh chúng với đại lượng cùng loại dược quy ước làm đơn vị.

+ Phép đo trực tiếp: giá trị của đại lượng cần đo được đọc trực tiếp trên dụng cụ đo (ví dụ như đo khối lượng bằng cân, đo thể tích bằng bình chia độ).

+ Phép đo gián tiếp: giá trị của đại lượng cần đo được xác định thông qua các đại lượng được đo trực tiếp (ví dụ như đo khối lượng riêng).

b. Các loại sai số của phép đo

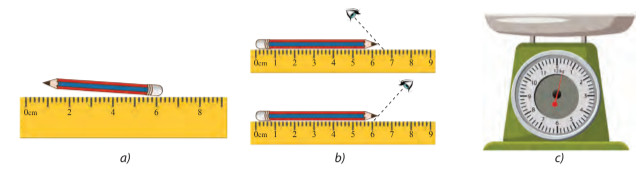
Hình 3.2. Một số nguyên nhân gây ra sai số khi đo

– Trong quá trình thực hiện phép đo, chúng ta không thể tránh khỏi sự chênh lệnh giữa giá trị thật và số đo giá trị đo được). Độ chênh lệch này gọi là sai số.

– Như vậy, mọi phép đo đều tồn tại sai số. Nguyên nhân gây ra sai số là do giới hạn về độ chính xác của dụng cụ đo, do kĩ thuật đo, quy trình đo, chủ quan của người đo,…

– Xét theo nguyên nhân thì sai số của phép đo được phân thành hai loại là sai số hệ thống và sai số ngẫu nhiên.

+ Sai số hệ thống là sai số có tính quy luật và được lặp lại ở tất cả các lần đo. Sai số hệ thống làm cho giá trị đo tăng hoặc giảm một lượng nhất định so với giá trị thực.

Sai số hệ thống thường xuất phát từ dụng cụ đo. Ngoài ra, sai số hệ thống còn xuất phát từ độ chia nhỏ nhất của dụng cụ đo (gọi là sai số dụng cụ). Đối với một số dụng cụ đo, sai số này thường được xác định bằng một nửa độ chia nhỏ nhất.
Trong thực hiện phép đo, cần tìm được nguyên nhân gây ra sai số hệ thống để tìm cách hạn chế. Sai số hệ thống có thể được hạn chế bằng cách thường xuyên hiệu chỉnh dụng cụ đo, sử dụng thiết bị đo có độ chính xác cao.

+ Sai số ngẫu nhiên là sai số xuất phát từ sai sót, phản xạ của người làm thí nghiệm hoặc từ những yếu tố ngẫu nhiên bên ngoài. Sai số này thường có nguyên nhân không rõ ràng và dẫn đến sự phân tán của các kết quả đo xung quanh một giá trị trung bình.

Ví dụ: Khi đo thời gian rơi của một vật bằng đồng hồ bấm giây, phản xạ của người đó sẽ gây ra sai số ngẫu nhiên. Khi đo khối lượng của một vật nhỏ bằng một cân hiện số có độ nhạy cao, các yếu tố khách quan như gió, bụi cũng có thể gây ra sai số ngẫu nhiên.
Sai số ngẫu nhiên có thể được hạn chế bằng cách thực hiện phép đo nhiều lần và lấy giá trị trung bình để hạn chế sự phân tán của số liệu đo.

c. Cách biểu diễn sai số của phép đo

– Khi tiến hành đo đạc, giá trị x của một đại lượng vật lí thường được ghi dưới dạng \(x = \overline x + \Delta x\) (3.1) với \(x = \overline x + \Delta x\) là giá trị trung bình của đại lượng cần đo khi tiến hành phép đo nhiều lần \(\overline x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}\) (3.2)

– Giá trị trung bình có thể xem là giá trị gần đúng nhất với giá trị thật của đại lượng vật li cần đo.

– Sai số của phép đo có thể biểu diễn dưới dạng:

+ Sai số tuyệt đối là \(\Delta x\) trong công thức (3.1).

Sai số tuyệt đối ứng với mỗi lần đo được xác định bằng trị tuyệt đối của hiệu giữa giá trị trung bình và giá trị của mỗi lán do. \(\Delta {x_i} = |\overline x – {x_i}|\) (3.3) với x_i là giá trị đo lần thứ i.
Sai số tuyệt đối trung bình của n lần đo được xác định theo công thức: \(\overline {\Delta x} = \frac{{\Delta {x_1} + \Delta {x_2} + … + \Delta {x_n}}}{n}\) (3.4)
Sai số tuyệt đối của phép đo cho biết phạm vi biến thiên của giá trị đo được và bằng tổng của sai số ngẫu nhiên và sai số dung cụ:
\(\Delta x = \overline {\Delta x} + \Delta {x_{dc}}\) (3.5)
Trong đó sai số dụng cụ \(\Delta {x_{dc}}\), thường được xem có giá trị bằng một nửa độ chia nhỏ nhất đối với những dụng cụ đơn giản như thước kẻ, cân bàn, bình chia độ,… Trong nhiều trường hợp, sai số dụng cụ thường được cung cấp chính xác bởi nhà sản xuất.

+ Sai số tương đối được xác định bằng tỉ số giữa sai số tuyệt đối và giá trị trung bình của đại lượng cần đo theo công thức: \(\delta x = \frac{{\Delta x}}{{\overline x }}.100\% \) (3.6)

Sai số tương đối cho biết mức độ chính xác của phép đo.

d. Cách xác định sai số trong phép đo gián tiếp

– Trong đa số trường hợp, một đại lượng cần đo (có giá trị F) được xác định gián tiếp thông qua việc đo trực tiếp những đại lượng khác (có giá trị x, y, z,…).

– Ví dụ: Khối lượng riêng được xác định bằng thương số của khối lượng và thể tích, chu vi hình chữ nhật được xác định bằng hai lần tổng của hai cạnh liên tiếp.

– Nguyên tắc xác định sai số trong phép đo gián tiếp như sau:

+ Sai số tuyệt đối của một tổng hay hiệu bằng tổng sai số tuyệt đối của các số hạng:

Nếu \(F = x \pm y \pm z\)… thì \(\Delta F = \Delta x + \Delta y + \Delta z\)

+ Sai số tương đối của một tích hoặc thương bằng tổng sai số tương đối của các thừa số:

Nếu \(F = {x^m}\frac{{{y^n}}}{{{z^k}}}\) thì \(\delta F = m.\delta x + n.\delta y + k.\delta z\)