– Tổng hợp lực là thay thế nhiều lực tác dụng đồng thời vào một vật bằng một lực có tác dụng giống hệt như tác dụng của những lực ấy. Lực thay thế này gọi là hợp lực, các lực được thay thế gọi là các lực thành phần.

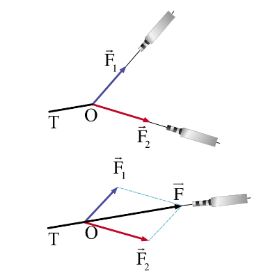
Lực F gây ra tác dụng lên dây cao su OT giống hệt khi F₁ và F₂ tác dụng đồng thời lên dây

1.1.1. Hai lực cùng phương

– Hai lực cùng phương, cùng chiều thì làm tăng tác dụng lên vật và có độ lớn hợp lực bằng: \(F = {F_1} + {F_2}\)

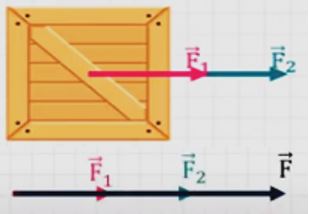
Hai lực cùng phương, cùng chiều

– Hai lực cùng phương, ngược chiều thì chúng hạn chế, thậm trí có thể triệt tiêu tác dụng của nhau lên vật

Hai lực cùng phương, ngược chiều

– Hợp lực có độ lớn bằng: \(F = {F_1} – {F_2}\)

+ Nếu F > 0 thì hợp lực F cùng chiều với lực thành phần F₁.

+ Nếu F < 0 thì lực F ngược chiều với lực F₁.

+ Ví dụ: Qủa bóng đang rơi như hình dưới đây:

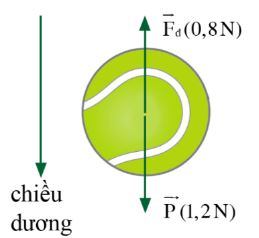
Hợp lực cùng phương, cùng chiều với trọng lực, cùng chiều dương đã chọn

1.1.2. Hai lực vuông góc

– Xét trường hợp một quả cầu lông đang rơi. Có hai lực tác dụng lên quả cầu: trọng lực theo phương thẳng đứng hướng xuống và lực đẩy của gió theo phương ngang.

– Hợp lực F tác dụng lên quả cầu được xác định bằng cách biểu diễn các lực thành phần P và Fđ  theo quy tắc cộng véctơ. Độ lớn hợp lực:

\(F = \sqrt {{P^2} + F_d^2} \)

– Hướng của hợp lực so với phương thẳng đứng là góc \(\theta \) sao cho:

\(\cos \theta  = \frac{P}{F}\)

– Ví dụ:

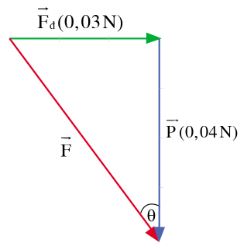
Tổng hợp hai lực vuông góc

1.1.3. Hai lực tạo với nhau một góc bất kì

– Các bước tổng hợp hai lực tạo với nhau một góc bất kì:

+ Bước 1: Vẽ hai vecto và đồng quy tai O

+ Bước 2: Vẽ một hình bình hành có hai cạnh liền kề trùng với hai veto và

+ Bước 3: Vẽ đường chéo hình bình hành có cùng gốc O. Vecto hợp lực F trùng với đường chéo này

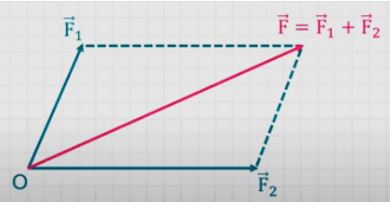
Tổng hợp hai lực tạo với nhau một góc bất kì

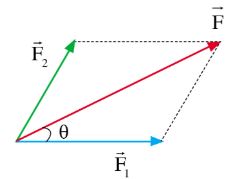
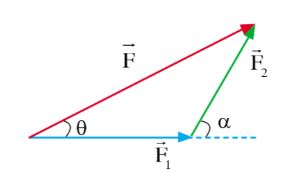
– Xét hai lực F1; F2 đồng quy và hợp thành góc \(\alpha \). Ta có thể biểu diễn lực theo quy tắc hình bình hành hoặc theo quy tắc cộng véctơ.

– Độ lớn của hợp lực: \({F^2} = F_1^2 + F_2^2 + 2{F_1}.{F_2}\cos \alpha \)

Tổng hợp hai lực đồng quy theo quy tắc hình bình hành	Tổng hợp hai lực đồng quy theo quy tắc cộng vecto

– Hướng của hợp lực so với F₁: \(\cos \theta  = \frac{{{F^2} + F_1^2 – F_2^2}}{{2F.{F_1}}}\)

– Lực F được phân tích thành hai thành phần vuông góc có giá trị tính bằng:

\({F_x} = F\cos \theta \) và \({F_y} = F\sin \theta \)

Với \(\theta \) là góc giữa hướng của lực F và hướng Ox (thường chọn trùng hướng chuyển động)

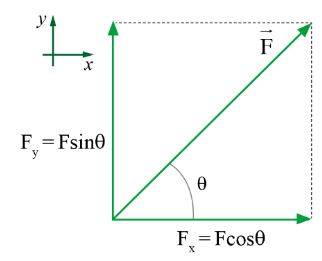
Phân tích lực F thành hai thành phần

– Ví dụ: Xét trường hợp ô tô đang lên dốc.

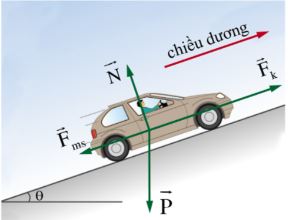
Các lực tác dụng ô tô đang lên dốc

– Các lực tác dụng lên ô tô gồm:

+ Trọng lực: P

+ Phản lực: N

+ Lực phát động: F_k

+ Lực ma sát: F_ms

– Các bước như sau:

+ Bước 1: Vẽ giản đồ các lực tác dụng lên vật.

+ Bước 2: Chọn chiều dương trùng với hướng chuyển động lên dốc của ô tô.

+ Bước 3: Phân tích trọng lực P thành hai thành phần

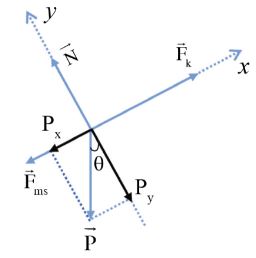
Phân tích trọng lực P thành hai thành phần

– Các bước thực hiện cũng áp dụng được cho trường hợp vật chịu tác dụng của nhiều lực nhưng vẫn đứng yên. Ngoài ra khi vật chuyển động thẳng đều cũng thu được kết quả tương tự.

– Trạng thái vật đứng yên hoặc chuyển động thẳng đều được gọi chung là trạng thái cân bằng của vật, đó là khi lực tổng hợp tác dụng lên vật bằng 0.

Hợp lực F của hai lực F1, F2 đồng quy, tạo với nhau góc \(\alpha \) có độ lớn được tính bằng  \({F^2} = F_1^2 + F_2^2 + 2{F_1}.{F_2}\cos \alpha \)  và có hướng so với hướng của lực F1 được xác định bởi \(\cos \theta  = \frac{{{F^2} + F_1^2 – F_2^2}}{{2F.{F_1}}}\) Lực F được phân tích thành hai thành phần vuông góc có giá trị tính bằng: \({F_x} = F\cos \theta \) và \({F_y} = F\sin \theta \) với \(\theta \) là góc giữa hướng của lực F và hướng Ox (thường chọn trùng hướng chuyển động).