Chuyển động thẳng với gia tốc không đổi được gọi là chuyển động thẳng biến đổi đều.

1.1.1. Công thức tính vận tốc

– Đồ thị vận tốc – thời gian biểu diễn chuyển động của một vật với vận tốc tăng dần đều từ v₀ đến v trong thời gian t.

– Quan sát hình dưới đây ta thấy:

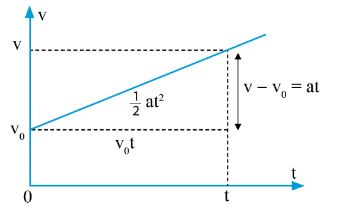
Tính vận tốc của chuyển động thẳng biến đổi đều

– Đồ thị là một đường thẳng, do đó gia tốc của vật không đổi

– Độ dốc của đường thẳng có giá trị bằng gia tốc

\(a = \frac{{v – {v_0}}}{t}\,\)

Công thức vận tốc trong chuyển động thẳng biến đổi đều: 

\(v = {v_0} + at\) (1)

Trong đó: 

v: vận tốc tại thời điểm t 

v₀: vận tốc tại thời điểm ban đầu t₀ = 0

a: gia tốc không đổi

1.1.2. Công thức tính độ dịch chuyển

– Vận tốc trung bình của vật bằng một nửa tổng vận tốc ban đầu và vận tốc cuối cùng của nó:

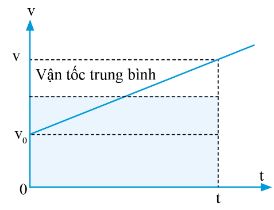
Tính độ dịch chuyển của chuyển động thẳng biến đổi đều

– Vận tốc trung bình: \({v_{tb}} = \frac{{{v_0} + v}}{2}\)

– Độ dịch chuyển = vận tốc trung bình x thời gian

⇒ Công thức tính độ dịch chuyển: \(d = \frac{{{v_0} + v}}{2} \times \,t\) (2)

1.1.3. Công thức tính quãng đường

Trong chuyển động thẳng theo một chiều xác định, độ dịch chuyển chính là quãng đường.

Ta có: 

\(v = {v_0} + at\) (1)

\(s = \frac{{{v_0} + v}}{2}xt\) (2)

Thay v từ công thức (1) vào công thức (2), ta được: 

\(\begin{array}{l}
s = \frac{{{v_0} + v + at}}{2}xt\\
 \Rightarrow s = {v_0}t + \frac{1}{2}a{t^2}
\end{array}\) (3) 

1.1.4. Công thức liên hệ quãng đường, vận tốc và gia tốc

Ta có: 

\(v = {v_0} + at \Rightarrow t = \frac{{v – {v_0}}}{a}\) (1′)   

\(s = \frac{{{v_0} + v}}{2}xt\) (2)

Thay t từ công thức (1’) vào (2), ta được: 

\(s = \frac{{{v_0} + v}}{2}x\frac{{v – {v_0}}}{a}\)

Hay:

\(s = \frac{{{v^2} – v_0^2}}{{2a}}\)

Từ đây ta có: 

\({v^2} – v_0^2 = 2as\) (4)

1.1.5. Ví dụ áp dụng các công thức chuyển động

Ví dụ: Một tên lửa được phóng từ trạng thái đứng yên với gia tốc 20 m/s². Tính vận tốc của nó sau 50s.

Hướng dẫn giải:

Áp dụng công thức v = v₀ + at

Thay giá trị v = 0 m/s + 20 m/s² x 50 s = 1 000 m/s

Vậy sau khi phóng 50 s, tên lửa sẽ bay với vận tốc 1 000 m/s = 3 600 km/h

1.2.1. Gia tốc rơi tự do

– Thí nghiệm sự rơi tự do: Quan sát video dưới đây về thí nghiệm sự rơi tự do

– Sự rơi của các vật khi chỉ chịu tác dụng của trọng lực được gọi là sự rơi tự do.

Khi quả bóng rơi, lực cản của không khí lên nó coi là nhỏ không đáng kể so với trọng lực tác dụng lên nó – coi là qủa bóng rơi tự do.

Ảnh hoạt nghiệm một quả bóng đang rơi

– Gia tốc của một vật rơi trên bề mặt Trái Đất có giá trị tùy thuộc vào vị trí mà vật rơi. Gia tốc này gọi là gia tốc rơi tự do, kí hiệu g; nó có chiều hướng thẳng đứng xuống dưới.

g = 9,81 m/s2

1.2.2. Đo gia tốc rơi tự do

Bộ dụng cụ đo gia tốc rơi tự do

(1) Nam châm điện (2) Viên bi thép (3) Cổng quang điện (4) Công tắc điều khiển (5) Đồng hồ đo thời gian (6) Giá

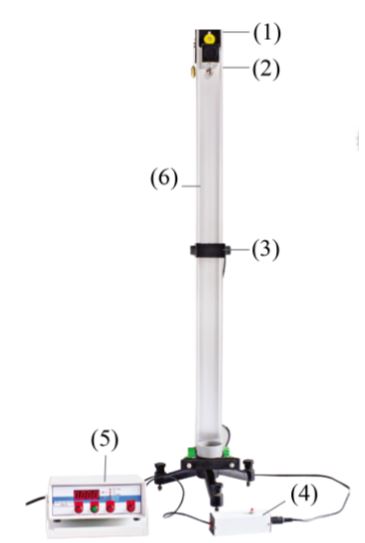
Bộ dụng cụ thí nghiệm đo gia tốc rơi tự do

Tùy vào điều kiện, cơ sở vật chất mà chúng ta sẽ có các bộ dụng cụ thí nghiệm đo gia tốc rơi tự do khác nhau.

Xét chuyển động của một vật có vận tốc ban đầu theo phương ngang hoặc xiên góc với phương ngang

1.3.1. Vận tốc ban đầu theo phương ngang

Hai quả bóng rơi chạm đất đồng thời

* Mô tả chuyển động 

– Hình trên mô tả quá trình chuyển động của hai quả bóng nhỏ giống nhau được thả từ 1 độ cao như nhau. 

– Quả bóng thứ nhất được thả rơi theo phương thẳng đứng, chuyển động nhanh dần xuống dưới; 

– Quả bóng thứ 2 được ném theo phương nằm ngang (quỹ đạo chuyển động có dạng đường cong. 

* Kết quả: Hai quả bóng chạm đất đồng thời 

=> Vận tốc theo phương ngang của quả bóng thứ 2 không ảnh hưởng đến chuyển động thẳng đứng của nó.

* Giải thích chuyển động:

– Hai quả bóng cùng có gia tốc thẳng đứng bằng nhau với giá trị là g 

– Lực tác dụng vào một vật có thể làm thay đổi cả tốc độ và hướng chuyển động của vật, tức là làm thay đổi vận tốc của vật. Nếu bỏ qua lực cản không khí thì theo phương nằm ngang không có lực nào tác dụng lên các quả bóng. Vì thế vận tốc theo phương này sẽ giữ nguyên giá trị ban đầu của nó.

⇒ Thời gian chạm đất của vật được ném ngang từ độ cao h: \(t = \sqrt {\frac{{2h}}{g}} \)

⇒ Tầm xa của vật ném ngang: \(L = {v_0}t = {v_0}\sqrt {\frac{{2h}}{g}} \)

1.3.2. Vận tốc ban đầu tạo góc xác định với phương ngang

Hình ảnh quả bóng nảy lên khi va chạm sàn

* Mô tả chuyển động:

– Hình trên cho thấy hình ảnh của một quả bóng được ném xuống sàn và nảy lên xiên góc với phương ngang 

– Theo phương thẳng đứng: quả bóng đi lên chậm dần, khi rơi xuống nhanh dần. 

– Theo phương ngang: quả bóng chuyển động đều sang phải. 

* Kết quả: Chuyển động thẳng đứng và chuyển động ngang của quả bóng độc lập với nhau.

* Giải thích chuyển động:

– Sau khi nảy lên, nếu bỏ qua lực cản của không khí, quả bóng chịu tác dụng của lực hấp dẫn, tức là trọng lực tác dụng lên nó hướng thẳng đứng xuống dưới. Vì vậy, quả bóng đi lên chậm dần, đi xuống nhanh dần. 

– Chuyển động ngang của quả bóng không bị ảnh hưởng bởi trọng lực. 

– Trong điều kiện không có lực cản của không khí, quả bóng có vận tốc không đổi theo phương ngang nên nó chuyển động đều sang phải.

– Các công thức chuyển động thẳng: \(\begin{array}{l} v = {v_0} + at\\ d = \frac{{{v_0} + v}}{2} \times {\mkern 1mu} t\\ s = {v_0}t + \frac{1}{2}a{t^2}\\ {v^2} – v_0^2 = 2as \end{array}\) – Khi bỏ qua sức cản, vật rơi trong không khí được coi là rơi tự do với gia tốc rơi tự do hướng thẳng đứng xuống dưới. – Độ cao và tầm xa của vật bị ném phụ thuộc vào góc giữa vận tốc ban đầu và phương nằm ngang