1.1. Ví dụ 1
Một con lắc đơn gồm vật nặng có kích thước nhỏ, có khối lượng m, treo ở đầu một sợi dây mềm không giãn có độ dài l và khối lượng không đáng kể (Hình 7.1). Đưa vật nặng ra khỏi vị trí cân bằng O sao cho dây treo hợp với QO một góc \({\alpha _0}({\alpha _0} \le {10^0})\) rồi thả nhẹ cho con lắc dao động điều hòa trên cung tròn AOB.
a, Tính thế năng của con lắc; động năng của vật ở các vị trí A, O, B và vị trí bất kì (li độ góc \(\alpha \)).
b, Ở vị trí nào động năng bằng thế năng?
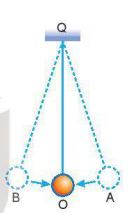
Hình 7.1
Giải:
a, Chọn mốc để tính thế năng của vật là vị trí cân bằng O thì:
– Thế năng và động nagw của vật tại vị trí A và B là:
\({W_t} = {W_{t\max }}mgl(1 – \cos {\alpha _0}) = mgl(2{\sin ^2}\frac{{\alpha _0^2}}{2}) \approx mgl\frac{{\alpha _0^2}}{2}\)
Wd = 0.
– Thế năng và động năng của vật ở vị trí O là:
Wt =0.
\({W_d} = {W_{t\max }} = mgl(1 – \cos {\alpha _0}) \approx mgl\frac{{\alpha _0^2}}{2}\)
– Thế năng và động năng của vật ở vị trí bất kì (li độ góc \(\alpha \)) là:
\({W_t} = mgl(1 – \cos {\alpha _0}) \approx mgl\frac{{{\alpha _0}^2}}{2}\) (với \(\alpha \) tính theo rad)
\({W_d} = {W_{t\max }} – {W_t} \approx mgl(\frac{{{\alpha _0}^2}}{2} – \frac{{{\alpha ^2}}}{2})\)
b, Khi Wd = Wt , áp dụng định luật bảo toàn cơ năng:
\(\begin{array}{l}
W = {W_{t\max }} = {W_d} + {W_t} = 2{W_t}\\
\Leftrightarrow mgl\frac{{\alpha _0^2}}{2} = 2mgl\frac{{{\alpha ^2}}}{2} \Rightarrow \alpha = \pm \frac{{{\alpha _0}}}{{\sqrt 2 }}
\end{array}\)
Vậy ở các vị trí có li độ góc \(\alpha = \pm \frac{{{\alpha _0}}}{{\sqrt 2 }}\) thì động năng bằng thế năng.
1.2. Ví dụ 2
Một vật có khối lượng m = 200 g dao động điều hòa với tần số góc \(\omega = 2\pi \) rad/s, biên độ A = 10 cm. Xác định thế năng của con lắc tại thời điểm vật có tốc độ v = 10 cm/s.
Giải:
Ta đã biết trong dao động điều hòa cơ năng được bảo toàn \({\rm{W}} = {W_t} + {W_{d’}}\)
Suy ra thế năng:
\({W_t} = W – {W_d} = \frac{{m{\omega ^2}{A^2}}}{2} – \frac{{m{v^2}}}{2} = \frac{m}{2}({\omega ^2}{A^2} – {v^2}) = \frac{{0,2}}{2}({2^2}.{\pi ^2}.{(0,1)^2} – {1^2}) = 0,038J\)
1.3. Ví dụ 3
Một con lắc lò xo có độ cứng k = 100 N/m dao động điều hòa. Gọi Wt, Wd lần lượt là thế năng của lò xo và động năng của vật, W0 là cơ năng của con lắc lò xo. Đồ thị biểu diễn sự phụ thuộc của thế năng Wt và động năng Wd của con lắc vào li độ x như Hình 7.2. Tính W0 .
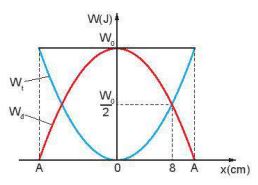
Hình 7.2
Giải:
Từ đồ thị ta xác định được:
Khi \(x = \pm 8cm = \pm 0,08cm\) thì Wt = Wd.
Mặc khác vì W0 = Wt + Wd nên khi Wt = Wd ta có:
\({{\rm{W}}_0} = 2{W_t} = 2.\frac{1}{2}k{x^2} = 0,64J\)