1.1.1. Phương trình của vận tốc

\(v =  – \omega A\sin (\omega t + \varphi )\)

Vận tốc của vật dao động điều hòa cũng biến thiên tuần hoàn theo quy luật hàm sin (cosin) cùng chu kì T của li độ

Độ lớn của vận tốc

\(\left| v \right| = \omega A\sqrt {1 – {{\cos }^2}(\omega t + \varphi )} \)

Thay \(\cos (\omega t + \varphi ) = \frac{x}{A}\) ta được

\(v =  \pm \omega \sqrt {{A^2} – {x^2}} \)

– Khi vật ở VTCB thì \(v =  \pm \omega A\)

– Khi vật ở vị trí biên thì \(v = 0\)

1.1.2. Đồ thị của vận tốc

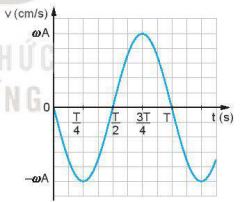
Hình 3.1. Đồ thị ( v – t ) của một vật dao động điều hòa ( \(\varphi  = 0\) )

Hình 3.1 là đồ thị vận tốc của một dao động điều hòa với \(\varphi  = 0\). Nó cũng là một đường hình sin.

1.2.1. Phương trình của gia tốc

\(a =  – {\omega ^2}A\cos (\omega t + \varphi )\)

Thay \(x = A\cos (\omega t + \varphi )\) ta được

\(a =  – {\omega ^2}x\)

– Khi vật ở VTCB \(a = 0\)$$

– Khi vật ở vị trí biên \(a =  \pm {\omega ^2}A\)

1.2.2. Đồ thị của gia tốc

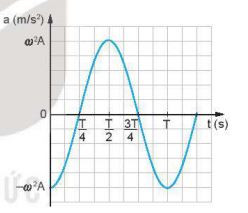
Hình 3.2. Đồ thị ( a – t ) của một vật dao động điều hòa ( \(\varphi  = 0\) )

Hình 3.2 là đồ thị gia tốc của một dao động điều hòa với \(\varphi  = 0\). Nó cũng là một đường hình sin như li độ và vận tốc.

– Phương trình của vận tốc và gia tốc của một vật dao động điều hòa có li độ là \(x = A\cos (\omega t + \varphi )\):                                            \(v =  – \omega A\sin (\omega t + \varphi )\)                                            \(a =  – {\omega ^2}A\cos (\omega t + \varphi )\) – Đồ thị của vận tốc, gia tốc theo thời gian là một đường hình sin. Vận tốc của một vật dao động sớm pha \(\frac{\pi }{2}\) so với li độ, còn gia tốc của vật dao động ngược pha so với li độ. – Vectơ gia tốc luôn hướng về vị trí cân bằng và có độ lớn tỉ lệ với độ lớn của li độ. – Tại vị trí biên, vận tốc của vật bằng 0, còn gia tốc của vật có độ lớn cực đại. Tại vị trí cân bằng, gia tốc của vật bằng 0 còn vận tốc của vật có độ lớn cực đại.