1.1. Ví dụ 1
Một sóng âm có tần số 192 Hz và truyền đi được quãng đường 91,4 m trong 0,27 s. Hãy tính
a) Tốc độ truyền sóng.
b) Bước sóng.
c) Nếu tần số sóng là 442 Hz thì bước sóng và chu kì là bao nhiêu?
Giải
a) \(v = \frac{s}{t} = \frac{{91,4}}{{0,27}} = 338,5m/s.\)
b) Sử dụng công thức v = λf
\( \Rightarrow \lambda = \frac{v}{f} = \frac{{338,5}}{{192}} = 1,76m.\)
c)\(\begin{array}{l}
\lambda ‘ = \frac{v}{{f’}} = \frac{{338,5}}{{442}} = 0,77m\\
T’ = \frac{1}{f} = \frac{1}{{442}} = 0,002s
\end{array}\)
1.2. Ví dụ 2
Trong thí nghiệm Hình 8.1, cần rung dao động với tần số 50 Hz. Người ta đo được bán kính của 2 gợn sóng hình tròn liên tiếp lần lượt bằng: 12,4 cm và 14,3 cm. Tính tốc độ truyền sóng.
Giải
Bước sóng là khoảng cách giữa hai gợn sóng liên tiếp, theo đề bài ta có:
λ = 14,3 – 12,4 = 1,9 cm;
Áp dụng công thức v = λf, tính tốc độ truyền sóng: v = 1,9.50 = 95 cm/s.
1.3. Ví dụ 3
Một sóng hình sin đang lan truyền từ trái sang phải trên một sợi dây dài Hình 14.1 là hình ảnh của sóng ở một thời điểm xét. Cho biết tốc độ truyền sóng v = 1 m/s.
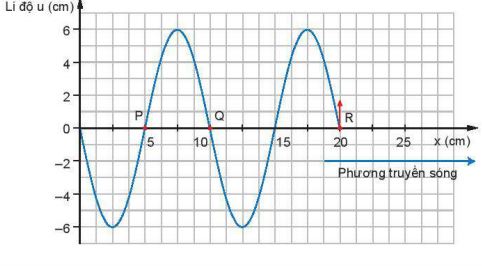
Hình 14.1
a) Tính tần số của sóng.
b) Hỏi điểm Q, P và 0 đang chuyển động lên hay xuống?
Giải
a) Từ đồ thị ta được λ = 10 cm = 0,1 m.
Sử dụng công thức: \(\lambda = \frac{v}{f}\)
Ta suy ra tần số của sóng: \(f = \frac{v}{\lambda } = \frac{1}{{0,1}}\) = 10 Hz.
b) Căn cứ vào sóng lan truyền tới điểm R bắt đầu đi lên.
– Điểm Q cách R đúng một bước sóng nên dao động cùng pha. Do vậy, tại điểm Q sóng phải bắt đầu chuyển động đi lên.
– Điểm P cách R 1,5 lần bước sóng nên dao động ngược pha. Do vậy, tại điểm P sóng phải bắt đầu chuyển động đi xuống.
– Điểm O cách R đúng hai bước sóng nên dao động cùng pha. Do vậy, tại điểm O sóng phải bắt đầu chuyển động đi lên.
1.4. Ví dụ 4
Trong một thí nghiệm về giao thoa ánh sáng với hai khe Y-âng, khoảng cách giữa hai khe hẹp là a = 2 mm, khoảng cách giữa mặt phẳng chứa hai khe với màn quan sát là D = 1,2 m. Khe sáng hẹp phát đồng thời hai bức xạ đơn sắc màu đỏ λ1 = 0,66 µm và màu lục λ2 = 0,55 µm.
a) Tính khoảng vân của hai ánh sáng màu đỏ và màu lục.
b) Tính khoảng cách ngắn nhất giữa hai vân sáng cùng màu với vân sáng trung tâm.
Giải
a) Với ánh sáng đỏ λ1 = 0,66 µm
\({i_1} = \frac{{{\lambda _1}D}}{a} = \frac{{0,{{66.10}^{ – 3}}.1,{{2.10}^3}}}{2} \approx 0,40mm.\)
Với ánh sáng lục λ2 = 0,55 µm
\({i_2} = \frac{{{\lambda _2}D}}{a} = \frac{{0,{{55.10}^{ – 3}}.1,{{2.10}^3}}}{2} \approx 0,35mm.\)
b)
Vân chính giữa ứng với k = 0 là chung cho cả hai bức xạ, tức là tại đó cả hai bức xạ đều cho vân sáng và vẫn có màu là màu hỗn hợp của màu đỏ và màu lục, tức là màu vàng – da cam.
Vân đầu tiên cùng màu với vân này ở tại điểm A và cách tâm 0 của vận chính giữa một khoảng x = OA sao cho: k1i1 = k2i2 với k \( \in \) Z
Ta nhận thấy 6k1 = 5k2.
Do vậy, giá trị nhỏ nhất của k1 là 5 và của k2 là 6, tức là:
OA = 0,33.6 = 1,98 mm