1.1. Khái niệm dao động tự do
a. Khái niệm dao động
– Dao động cơ học là sự chuyển động có giới hạn trong không gian của một vật quanh một vị trí xác định. Vị trí đó gọi là vị trí cân bằng
– Dao động mà trạng thái chuyển động của vật (vị trí và vận tốc) được lặp lại như cũ sau những khoảng thời gian bằng nhau được gọi là dao động tuần hoàn
Ví dụ: dao động của quả lắc đồng hồ
b. Dao động tự do
– Dao động của hệ xảy ra dưới tác dụng chỉ của nội lực được gọi là dao động tự do (dao động riêng)
1.2. Dao động điều hòa
a. Thí nghiệm khảo sát sự phụ thuộc tọa độ của vật dao động theo thời gian

Hình 1.1. Thí nghiệm khảo sát sự phụ thuộc tọa độ của vật dao động theo thời gian
– Hệ thống giá đỡ (1) và con lắc lò xo (2).
– Cảm biến khoảng cách (3).
– Dây cáp nối cảm biến với bộ ghi số liệu (4).
– Bộ ghi số liệu (5).
– Dây cáp nối bộ ghi số liệu và máy tính (6), máy tính (7).
b. Li độ, biên độ, chu kì dao động, tần số dao động
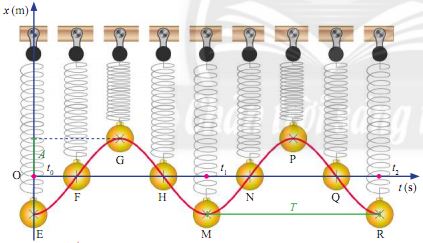
Hình 1.2. Vị trí của vật nặng trong hệ con lắc lò xo tại các thời điểm khác nhau
Chọn hệ trục tọa độ Oxt như hình 1.2
– Li độ của vật dao động là tọa độ của vật mà gốc tọa độ được chọn trùng với VTCB. Biên độ là độ lớn cực đại của li độ
– Chu kì dao động là khoảng thời gian để vật thực hiện được một dao động, đơn vị: giây (s)
– Tần số dao động được xác định bởi số dao động mà vật thực hiện được trong một giây, đơn vị: héc (Hz)
\(f = \frac{1}{T}\)
c. Khái niệm dao động điều hòa
Dao động điều hòa là dao động tuần hoàn mà li độ của vật dao động là một hàm côsin (hoặc sin) theo thời gian
d. Pha dao động, độ lệch pha, tần số góc
– Pha dao động là một đại lượng đặc trung cho trạng thái của vật trong quá trình dao động
– Độ lệch pha giữa hai dao động điều hòa cùng chu kì (cùng tần số) được xác định theo công thức:
\({\rm{\Delta }}\varphi = 2\pi \frac{{{\rm{\Delta }}t}}{T}\)
– Tần số góc của dao động là đại lượng đặc trưng cho tốc độ biến thiên của pha dao động. Đối với dao động điều hòa tần số góc có giá trị không đổi và được xác định theo công thức
\(\omega = \frac{{{\varphi _2} – {\varphi _1}}}{{{t_2} – {t_1}}} = \frac{{2\pi }}{T}\)
e. Vận dụng các đại lượng vật lí đặc trưng để mô tả dao động điều hoà
Ví dụ
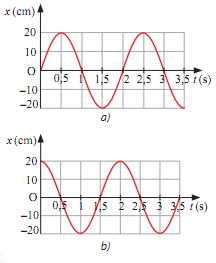
Hình 1.3. Đồ thị li độ – thời gian của một vật được kích thích dao động theo hai cách khác nhau
Hướng dẫn giải
Hình 1.3 thể hiện đô thị li độ – thời gian của một vật dao động điều hoà được kích thích theo hai cách khác nhau. Hãy xác định các đại lượng biên độ, chu kì, tần số và tần số góc trong từng trường hợp.
– Trong trường hợp a), vật bắt đầu dao động từ vị trí cân bằng theo chiều dương quy ước.
– Trong trường hợp b), vật bắt đầu dao động từ vị trí biên dương, ngược chiều dương quy ước.
– Trong hai trường hợp a) và b):
+ Vật dao động cùng biên độ A = 20 cm.
+ Vật dao động cùng chu kì T = 2 s.
+ Tần số dao động của vật trong cả hai trường hợp:
\(f = \frac{1}{T} = \frac{1}{2} = 0,5Hz\)
+ Tần số góc của vật trong cả hai trường hợp:
\(\omega = 2\pi f = 2\pi .0,5 = \pi Hz\)