1.1.1. Thí nghiệm tạo dao động

Hình 1.1. Quả cầu được treo bằng sợi dây

Dụng cụ

Quả cầu kim loại nhỏ, sợi dây mảnh nhẹ, giá thí nghiệm.

Tiến hành

+ Treo quả cầu vào giả thí nghiệm.

+ Khi quả cầu đứng yên tại vị trí cân bằng, dây treo có phương thẳng đứng, kéo quả cầu khỏi vị trí cân bằng một đoạn nhỏ rồi buông tay cho quả cầu chuyển động (Hình 1.2).

+ Mô tả chuyển động của quả cầu.

– Chuyển động qua lại quanh một vị trí cân bằng được gọi là dao động.

1.1.2. Dao động tự do

– Vật dao động với biên độ và tần số riếng (kí hiệu là f0) không đổi gọi là dao động tự do

1.1.3. Biên độ, chu kì, tần số của dao động

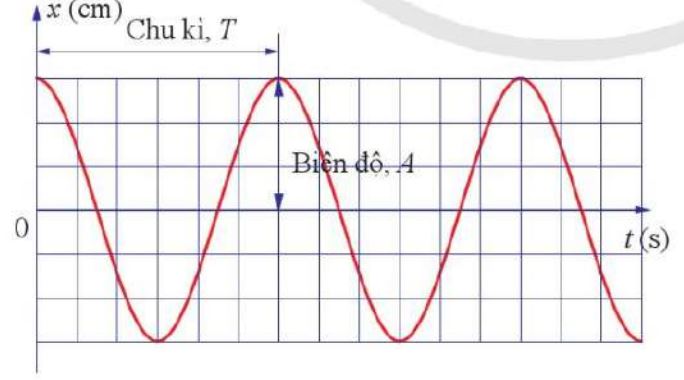
Hình 1.2. Đồ thị mô tả sự liên hệ giữa li độ và thời gian của xe kĩ thuật số.

– Độ lớn cực đại của độ dịch chuyển (độ lớn cực đại của li độ) được gọi là biên độ dao động, kí hiệu A

– Khoảng thời gian để vật thực hiện một dao động được gọi là chu kì của dao động, kí hiệu là T, đơn vị: giây (s)

– Số dao động thực hiện được trong một giâu được gọi là tần số của dao động, kí hiệu là f, đơn vị: Hertz (Hz)

1.2.1. Định nghĩa

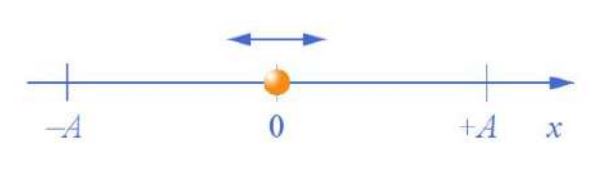
Hình 1.3. Một vật dao dộng điều hòa theo trục x, giữa hai giá trị x = +A và x = -A.

– Dao động điều hòa là dao động trong đó li độ của vật là một hàm côsin (hoặc sin) của thời gian

– Phương trình của dao động điều hòa: \(x = A\cos (\omega t + \varphi )\)

1.2.2. Tần số góc

– \(\omega = \frac{{2\pi }}{T} = 2\pi f\) được gọi là tần số góc của dao động, đơn vị: radian trên giây (rad/s)

1.2.3. Vận tốc và gia tốc trong dao động điều hòa

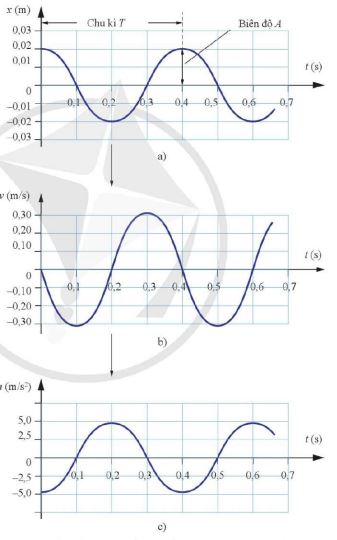
Hình 1.4. Đồ thị li độ, vận tốc, gia tốc theo thời gian của một vật dao động điều hoà

– Biểu thức của vận tốc và gia tốc lần lượt là:

\(v = – \omega A\sin (\omega t + \varphi )\)

\(a = – {\omega ^2}A\cos (\omega t + \varphi )\)

– Vận tốc và gia tốc của vật dao động điều hòa cũng biến thiên theo quy luật hàm số sin (côsin) cùng chu kì T của li độ

– Mối liên hệ giữa gia tốc và li độ của vật dao động điều hòa: \(a = – {\omega ^2}x\)

– Ở vị trí biên (\(x = \pm A\)): v=0; a=∓a_max=∓ω²A

– Ở vị trí cân bằng (x=0): v=± v_max=±ωA; a=0

1.2.4. Pha của dao động và độ lệch pha

a. Pha của dao động

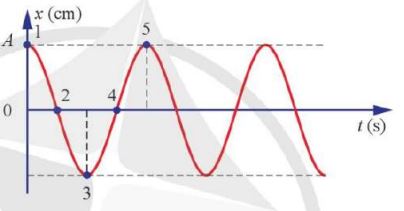
Hình 1.5. Trên đồ thị li độ – thời gian, đoạn 1-2-3-4-5 mô tả một dao động của vật.

– Pha của dao động tại một thời điểm được tính bằng số phần đã thực hiện của một chu kì, kể từ khi bắt đầu chu kì đó, được đo bằng đơn vị radian

– (ωt+φ) là pha dao động của dao động điều hòa tại thời điểm t

– Tại t=0, pha của dao động là φ, do đó φ là pha ban đầu của dao động

b. Dao động cùng pha

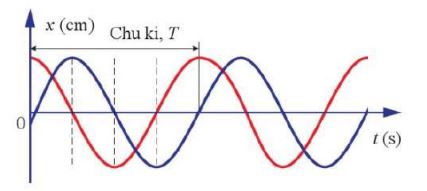
Hình 1.6. Đồ thị li độ – thời gian của hai dao động cùng pha

– Tại mỗi thời điểm, hai vật dao động đều có trạng thái giống nhau

c. Dao động lệch pha

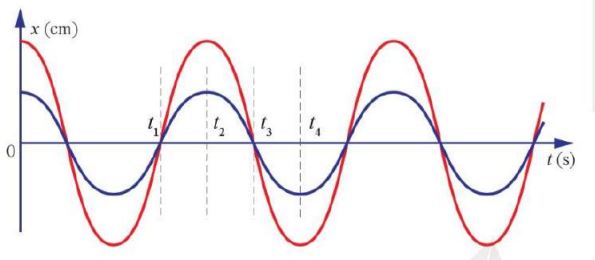
Hình 1.7. Đồ thị li độ – thời gian của hai dao động lệch pha nhau

– Độ lệch pha của hai vật dao động không đổi khi chúng dao động, luôn ứng với một phần của chu kì, tức là bằng \(\frac{{\Delta t}}{T}\)

• Dao động là chuyển động lập đi, lập lại quanh một vị trí cân bằng. • Biên độ của dao động là độ dịch chuyển lớn nhất của vật dao động so với vị trí cân bằng, kí hiệu là A. – Chu kì của dao động là khoảng thời gian để vật thực hiện một dao động, kí hiệu là T. • Đơn vị của chu kì là giấy. • Tần số của dao động là số dao động vật thực hiện được trong một giãy, kí hiệu là f. • Đơn vị của tần số là hertz (kí hiệu là Hz). • Độ lệch pha giữa hai dao động đo bằng số phần của một chu kì dao động. • Dao động điều hoà là dao động trong đó li độ của vật là một hàm côsin (hoặc sin) theo thời gian Trong đó \(x = A\cos (\omega t + \varphi )\) +x là li độ của dao động. + A là biên độ của dao động, + t là tần số góc của dao động, có đơn vị là rad/s, + \((\omega t + \varphi )\) là pha của dao động, có đơn vị là rad, + \(\varphi \) là pha ban đầu của dao động, có đơn vị là rad. • Tần số góc của dao động điều hoà liên hệ với chu kì Thoặc với tần số f bằng các hệ thức: \(\omega = \frac{{2\pi }}{T} = 2\pi f\) • Vận tốc và gia tốc của vật dao động điều hoà biến thiên tuần hoàn theo quy luật dạng sin với cùng chu kì T của li độ: \(v = – \omega A\sin (\omega t + \varphi )\) \(a = – {\omega ^2}A\cos (\omega t + \varphi )\) • Mối liên hệ giữa gia tốc a và li độ x của vật dao động điều hoa là: \(a = – {\omega ^2}x\)