– Số phức \(z = a + bi\) có phần thực là \(a\), phần ảo là \(b\) (\(a,b\in\mathbb{R}\) và \(i^2=-1\)).

– Số phức bằng nhau \(a + bi = c + di \Leftrightarrow\) \(a=c\) và \(b=d.\)

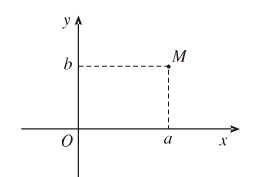
– Số phức \(z = a + bi\) được biểu diễn bới điểm \(M(a,b)\) trên mặt phẳng toạ độ.

 

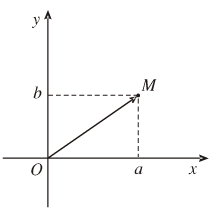
– Độ dài của vectơ \(\overrightarrow {OM} \) là môđun của số phức \(z\), kí hiệu là \(\left| z \right| = \overrightarrow {OM} = \sqrt {{a^2} + {b^2}} .\)

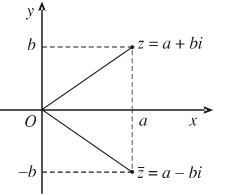
– Số phức liên hợp của số phức \(z = a + bi\) là \(a-bi\) kí hiệu là \(\overline z = a – bi.\)

– Mỗi số thực là số phức có phần ảo bằng 0. Ta có \(\mathbb{R}\subset \mathbb{C}.\)

– Số phức \(bi\)(\(b\in\mathbb{R}\)) được gọi là số thuần ảo (phần thực bằng 0).

– Số \(i\) được gọi là đơn vị ảo.

– Số phức viết dưới dạng \(z = a + bi(a,b\in\mathbb{R})\) gọi là dạng đại số của số phức.

– Ta có:

+ ​\(\left| {\overline z } \right| = \left| z \right|\).

+ \(z = \overline z \Leftrightarrow z\) là số thực.

+ \(z = – \overline z \Leftrightarrow z\) là số ảo.