1.1. Đường thẳng song song với mặt phẳng

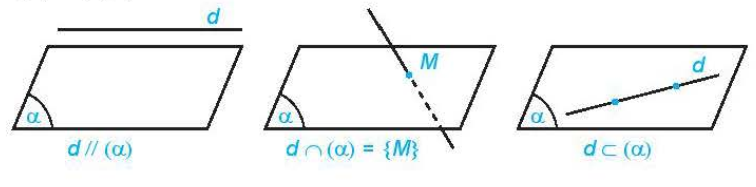
Cho đường thẳng d và mặt phẳng (\(\alpha\)). Nếu d và (\(\alpha\)) không có điểm chung thì ta nói d song song với (\(\alpha\)) hay (\(\alpha\)) song song với d và kí hiệu là d // (\(\alpha\)) hay (\(\alpha\)) // d.

 

Ngoài ra:

– Nếu d và (\(\alpha\)) có một điểm chung duy nhất M thì ta nói d và (\(\alpha\)) cắt nhau tại điểm M và kí hiệu d \(\cap\) (\(\alpha\)) = {M} hay d \(\cap\) (\(\alpha\)) = M.

– Nếu d và (\(\alpha\)) có nhiều hơn một điểm chung thì ta nói d nằm trong (\(\alpha\)) hay (\(\alpha\)) chứa d và kí hiệu d \(\subset\) (\(\alpha\)) hay (\(\alpha\)) \(\supset\) d.

1.2. Điều kiện và tính chất của đường thẳng song song với mặt phẳng

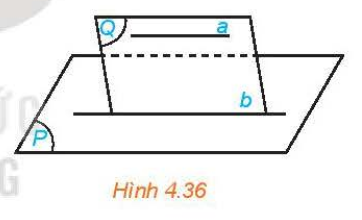
– Nếu đường thằng a không nằm trong mặt phẳng (P) và song song với một đường thẳng nằm trong (P) thì a song song với (P).

 

– Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thi b song song với a.