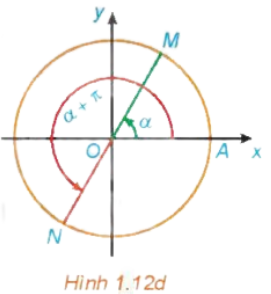
1.1. Góc lượng giác
a) Khái niệm góc lượng giác và số đo của góc lượng giác
|
Trong mặt phẳng, cho hai tia Ou, Ov. Xét tia Om cùng nằm trong mặt phẳng này. Nếu tia Om quay quanh điểm O, theo một chiều nhất định từ Ou đến Ov, thì ta nói nó quét một góc lượng giác với tia đầu Ou, tia cuối Ov. Kí hiệu là (Ou,Ov). |
Ta quy ước: Chiều quay ngược với chiều quay của kim đồng hồ là chiều dương, chiều quay cùng chiều kim đồng hồ là chiều âm.
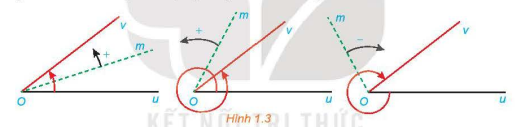
Khi đó, nếu tia Om
– quay theo chiều dương đúng một vòng ta nói tia Om quay góc 360°,
– quay theo chiều dương đúng 2 vòng ta nói nó quay góc 720,
– quay theo chiều âm nửa vòng ta nói nó quay góc –180°,
– quay theo chiều âm 1,5 vòng ta nói nó quay góc -1,5 . 360° = -540°, …
Số đo của góc lượng giác có tia đầu Ou, tia cuối Ov. Kí hiệu là sđ (Ou,Ov).
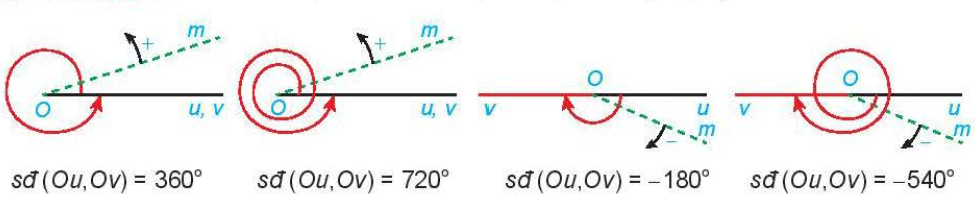
Mỗi góc lượng giác gốc O được xác định bởi tia đầu Ou, tia cuối Ov và số đo của nó.
Chú ý.
– Cho hai tia Ou, Ov thi có vô số góc lượng giác tia đầu Ou, tia cuối Ov.
– Mỗi góc lượng giác như thế đều kí hiệu là (Ou,Ov).
– Số đo của các góc lượng giác này sai khác nhau một bội nguyên của 360°.
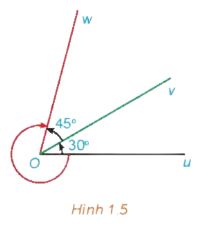
b) Hệ thức Chasles
|
Hệ thức Chasles: Với ba tia Ou, Ov, Ow bất kì, ta có sđ(Ou, Ov) + sđ(Ov, Ow) = sđ(Ou,Ow) + k360° (k ∈ Z). |
Nhận xét. Từ hệ thức Chasles, ta suy ra:
Với ba tia tuỳ ý Ox, Ou, Ov ta có:
sđ(Ou, Ov) = sđ(Ox, Ov) – sđ(Ox, Ou) + k360° (k ∈ Z).
Hệ thức này đóng vai trò quan trọng trong việc tính toán số đo của góc lượng giác.
1.2. Đơn vị đo góc và độ dài cung tròn
a) Đơn vị đo góc và cung tròn
– Đơn vị độ: Góc 1° bằng \(1\over 180\) góc bẹt.
Đơn vị độ được chia thành những đơn vị nhỏ hơn: 1° = 60’; 1’ = 60″.
– Đơn vị rađian: Cho đường tròn (O) tâm O, bán kính R và một cung AB trên (O) (H.1.6).
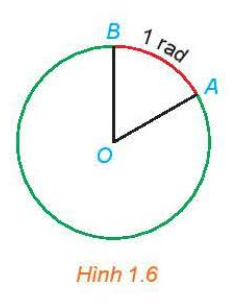
Cung tròn AB có số đo bằng 1 radian nếu độ dài của nó đúng bằng bán kính R.
Khi đó, góc AOB có số đo bằng 1 rađian và viết: \(\widehat{AOB}\) = 1 rad.
Quan hệ giữa độ và radian:
|
360° = \(2\pi\) rad. 1° = \(\pi\over 180\) rad và 1 rad = \({180\over \pi}^°\) |
Chú ý: Khi viết số đo của một góc theo đơn vị rađian, người ta thường không viết chữ rad sau số đo. Chẳng hạn góc \(\pi\over 2\) được hiểu là góc \(\pi\over 2\) rad.
Bảng tương ứng giữa độ và rađian của các góc đặc biệt trong phạm vi từ 0° đến 180°
|
Độ |
0° |
30° |
45° |
60° |
90° |
120° |
135° |
150° |
180° |
|
Rađian |
0 |
\(\pi\over 6\) |
\(\pi\over 4\) |
\(\pi\over 3\) |
\(\pi\over 2\) |
\(2\pi\over 3\) |
\(3\pi\over 4\) |
\(5\pi\over 6\) |
\(\pi\) |
b) Độ dài cung tròn
| Một cung của đường tròn bán kính R và có số đo \(\alpha\) rad thì có độ dài l = R\(\alpha\). |
1.3. Giá trị lượng giác của góc lượng giác
a) Đường tròn lượng giác
– Đường tròn lượng giác là đường tròn có tâm tại gốc toạ độ, bán kính bảng 1, được định hướng và lấy điểm A(1; 0) làm điểm gốc của đường tròn.
– Điểm trên đường tròn lượng giác biểu diễn góc lượng giác có số đo a (độ hoặc rađian) là điểm M trên đường tròn lượng giác sao cho sđ (OA, OM) = \(\alpha\).
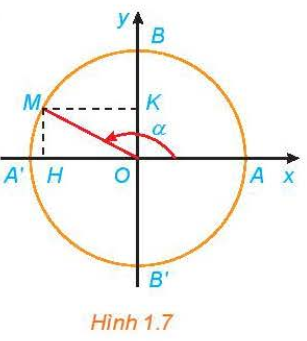
b) Các giá trị lượng giác của góc lượng giác
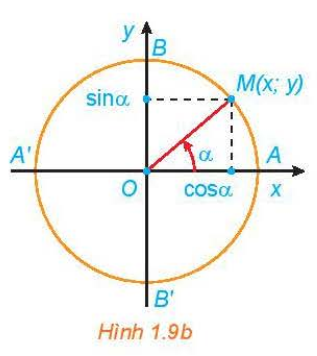
Ta có thể mở rộng khái niệm giá trị lượng giác cho các góc lượng giác có số đo tuỳ ý như sau: Giả sử M(x; y) là điểm trên đường tròn lượng giác, biểu diễn góc lượng giác có số đo \(\alpha\).
|
– Hoành độ x của điểm M được gọi là côsin của \(\alpha\), kí hiệu là cos\(\alpha\). cos\(\alpha\) = x. – Tung độ y của điểm M được gọi là sin của \(\alpha\), kí hiệu là sin\(\alpha\). sin\(\alpha\) = y. – Nếu cos α ≠ 0, tỉ số \(\sin \alpha \over \cos \alpha\) được gọi là tang của \(\alpha\), kí hiệu là tan\(\alpha\). \(\tan\alpha = {\sin \alpha \over \cos \alpha} = {y \over x}, \quad (x\ne 0)\). – Nếu sina ≠ 0, tỉ số \(\cos \alpha \over \sin \alpha\) được gọi là côtang của \(\alpha\), kí hiệu là cot\(\alpha\). \(\cot\alpha = {\cos \alpha \over \sin \alpha} = {x \over y}, \quad (y\ne 0)\). – Các giá trị cos \(\alpha\), sin\(\alpha\), tan\(\alpha\), cot\(\alpha\) được gọi là các giá trị lượng giác của \(\alpha\). |
Chú ý
– Ta còn gọi trục tung là trục sin, trục hoành là trục côsin,
– Từ định nghĩa ta suy ra
+) sin \(\alpha\), cos \(\alpha\) xác định với mọi giá trị của \(\alpha\) và ta có:
-1 ≤ sin\(\alpha\) ≤ 1;
-1 ≤ cos\(\alpha\) ≤ 1;
\(\sin (\alpha +k2\pi)=\sin \alpha\);
\(\cos (\alpha +k2\pi)=\cos \alpha\).
+) tan \(\alpha\) xác định khi \(\alpha\ne {\pi\over 2} + k\pi, (k\in \mathbb{Z})\).
+) cot\(\alpha\) xác định khi \(\alpha\ne {\pi} + k\pi, (k\in \mathbb{Z})\).
Dấu của các giá trị lượng giác của một góc lượng giác (H.1.10).
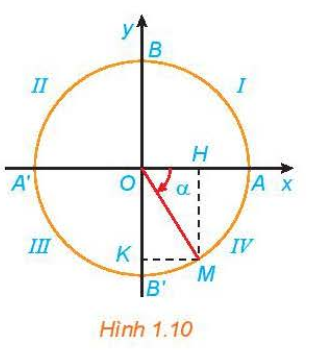
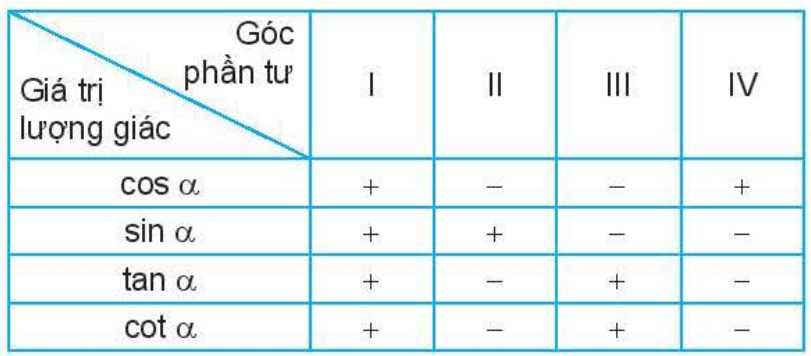
c) Giá trị lượng giác của các góc đặc biệt
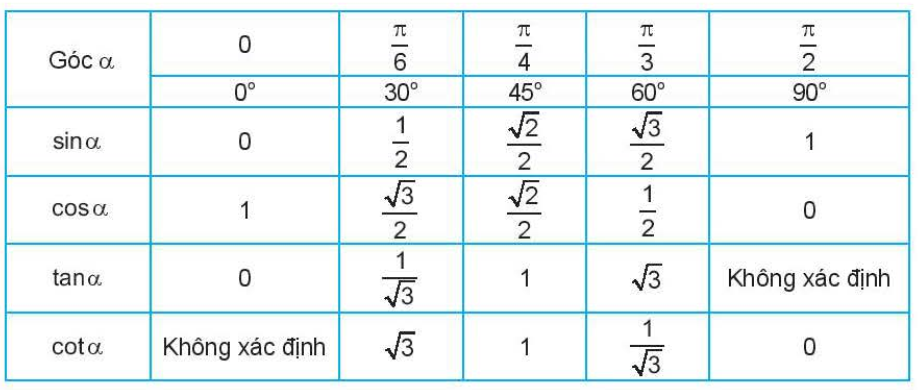
d) Sử dụng máy tính cầm tay để đổi số đo góc và tìm giá trị lượng giác của góc
Có thể dùng máy tính cầm tay để tính giá trị lượng giác của góc lượng giác và đổi số đo độ của cung tròn ra rađian và ngược lại.
Ví dụ. Sử dụng máy tính cầm tay để tính: sin chữ số thập phân thứ tư).
Giải
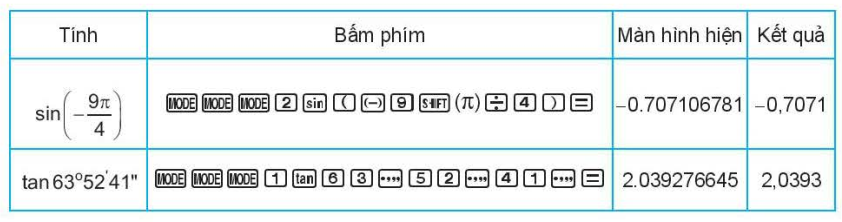
1.4. Quan hệ giữa các giá trị lượng giác
a) Các công thức lượng giác cơ bản
Đối với các giả trị lượng giác, ta có các hệ thức cơ bản sau
|
\(\begin{array}{l} {\sin ^2}a + {\cos ^2}a = 1\\ 1 + {\tan ^2}a = \frac{1}{{{{\cos }^2}a}}\left( {a \ne \frac{\pi }{2} + k\pi ,k \in Z} \right)\\ 1 + {\cot ^2}a = \frac{1}{{{{\sin }^2}a}}\left( {a \ne k\pi ,k \in Z} \right)\\ \tan a.\cot a = 1 \end{array}\) |
b) Giá trị lượng giác của các góc có liên quan đặc biệt
– Góc đối nhau: a và – a.
|
\(\cos \left( { – a} \right) = \cos a\\ \sin \left( { – a} \right) = – \sin a\\ \tan \left( { – a} \right) = – \tan a\\ \cot \left( { – a} \right) = – \cot a.\) |
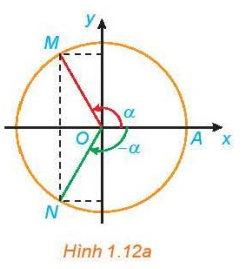
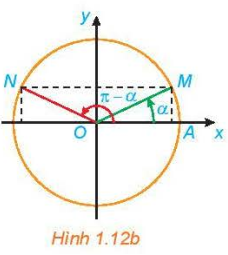
– Góc bù nhau: a và \(\pi { – a}\).
|
\(\sin \left(\pi { – a} \right) = \sin a\\ \cos \left(\pi { – a} \right) = -\cos a\\ \tan \left(\pi { – a} \right) = – \tan a\\ \cot \left(\pi { – a} \right) = – \cot a.\) |
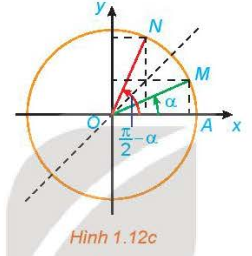
– Góc phụ nhau: a và \({\pi \over 2} { – a} \).
|
\(\sin \left({\pi \over 2} { – a} \right) = \cos a\\ \cos \left({\pi \over 2} { – a} \right) = \sin a\\ \tan \left({\pi \over 2} { – a} \right) = \cot a\\ \cot \left({\pi \over 2} { – a} \right) = \tan a.\) |
– Góc hơn kém \(\pi\): a và \({\pi} { a} \).
|
\(\sin \left(\pi {+ a} \right) = – \sin a\\ \cos \left(\pi { + a} \right) = -\cos a\\ \tan \left(\pi {+a} \right) = \tan a\\ \cot \left(\pi {+ a} \right) = \cot a.\) |