1.1. Phương trình mũ
Phương trình dạng \(a^x=b\), trong đó a và b là những số cho trước, a > 0, \(a \ne 1\), được gọi là phương trình mũ cơ bản.
Nghiệm của phương trình mũ cơ bản
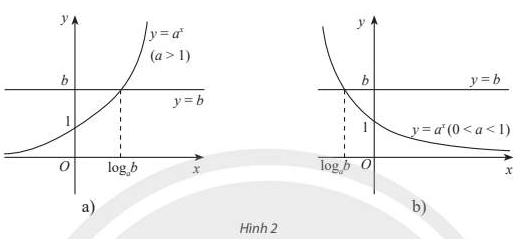
Cho phương trình mũ \(a^x=b\) (với \(0 < a \ne 1\)).
– Nếu b > 0 thì phương trình luôn có nghiệm duy nhất \(x = log_a b\).
– Nếu b ≤ 0 thì phương trình vô nghiệm.
Chú ý:
+) Nếu\(b = a^\alpha\) thì ta có \(a^x=a^\alpha \Leftrightarrow x= \alpha \).
+) Tổng quát hơn, \(a^{u(x)}=a^{v(x)} \Leftrightarrow u(x)=v(x)\) .
1.2. Phương trình lôgarit
Phương trình dạng \(\log_a x = b\), trong đó a, b là những số cho trước, a > 0, \(a \ne 1\), được gọi là phương trình lôgarit cơ bản.
Nghiệm của phương trình lôgarit cơ bản
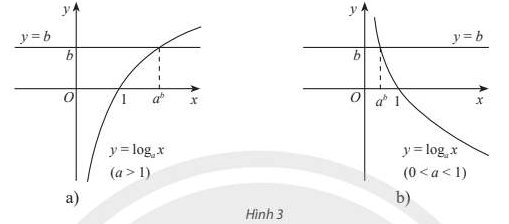
Phương trình \(\log_a x = b\) (\(0< a \ne 1\)) luôn có nghiệm duy nhất \(x = a^b\)
Chú ý: Tổng quát, xét phương trình dạng
\(\log_a u(x) = \log_a v(x)\) (\(a > 0, a \ne 1\)). (1)
Để giải phương trình (1), trước hết cần đặt điều kiện có nghĩa: u(x) > 0 và v(x) > 0. Khi đó, (1) được biến đổi thành phương trình
u(x) = v(x). (2)
Sau khi giải phương trình (2), ta cần kiểm tra sự thoả mãn điều kiện. Nghiệm của phương trình (1) là những nghiệm của (2) thoả mãn điều kiện.
1.3. Bất phương trình mũ
Bất phương trình mũ cơ bản có dạng \(a^x > b\) (hoặc \(a^x \ge b\), \(a^x < b\), \(a^x \le b\)) với \(a>0, a \ne 1\).
Xét bất phương trình dạng \(a^x > b\) (3)
– Nếu b ≤ 0 thì tập nghiệm của bất phương trình là R.
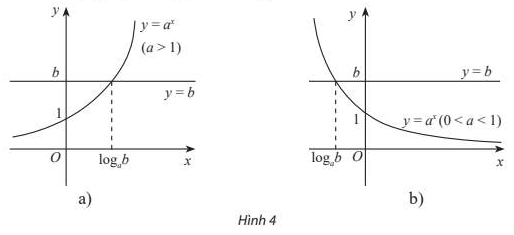
– Nếu b > 0 thì bất phương trình tương đương với \(a^x > a^{\log_a b}\).
+ Với a > 1, nghiệm của bất phương trình là x > \(\log_a b\).
+ Với 0 < a < 1, nghiệm của bất phương trình là x < \(\log_a b\).
Chú ý:
+) Tương tự như trên, từ đồ thị ở Hình 4, ta nhận được kết quả về nghiệm của mỗi bất phương trình \(a^x \ge b\), \(a^x < b\), \(a^x \le b\) (các bất phương trình \(a^x < b\), \(a^x \le b\) vô nghiệm nếu b ≤ 0).
+) Nếu a > 1 thì \(a^{u(x)} > a^{v(x)} \Leftrightarrow {u(x)} > v(x)\).
Nếu 0 < a < 1 thì \(a^{u(x)} > a^{v(x)} \Leftrightarrow {u(x)} < v(x)\).
1.4. Bất phương trình Lôgarit
Bất phương trình lôgarit cơ bản có dạng \(\log_a x > b\) (hoặc \(\log_a x \ge b\), \(\log_a x < b\), \(\log_a x \le b\)) với \(a>0, a \ne 1\).
Xét bất phương trình dạng \(\log_a x > b\).
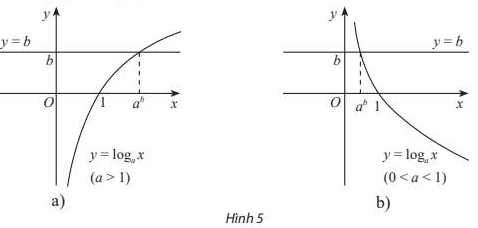
– Nếu a > 1 thì nghiệm của bất phương trình là \(x > a^b\).
– Nếu 0 < a < 1 thì nghiệm của bất phương trình là \(0 < x < a^b\).
Chú ý:
+) Tương tự như trên, từ đồ thị ở Hình 5, ta nhận được kết quả về nghiệm của mỗi bất phương trình \(\log_a x \ge b\), \(\log_a x < b\), \(\log_a x \le b\).
+) Nếu a > 1 thì \(\log_a u > \log_a v \Leftrightarrow u > v > 0\).
Nếu 0 < a < 1 thì \(\log_a u(x) > \log_a v(x) \Leftrightarrow 0 < u(x) < v(x)\).