1.1. Đạo hàm của hàm số \(y = x^n, n\in N^*\)
Hàm số \(y = {x^n}(n \in \mathbb{N},n > 1\)) có đạo hàm với mọi \(x \in\mathbb{R}\) và: \({\left( {{x^n}} \right)’} = n{x^{n – 1}}.\)
1.2. Đạo hàm của hàm số \(y=\sqrt x\)
Hàm số \(y= \sqrt x\) có đạo hàm với mọi x dương và: \(\left( {\sqrt x } \right)’ = \frac{1}{{2\sqrt x }}.\)
1.3. Đạo hàm của hàm số lượng giác
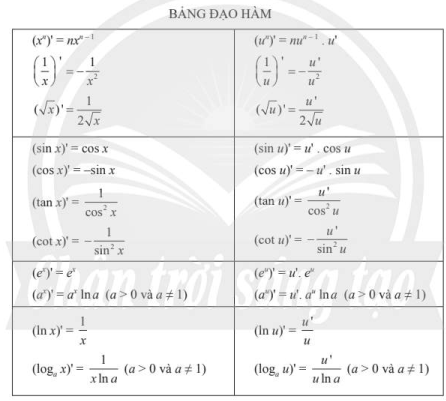
Ta có công thức đạo hàm của các hàm số lượng giác sau:
\(\begin{array}{l}(\sin x)’ = \cos x\\ ( \cos x )’ = – \sin x\\{\left( {\tan x} \right)’} = \frac{1}{{{{\cos }^2}x}} &\\ {\left( {\cot x} \right)’} = – \frac{1}{{{{\sin }^2}x}} & \end{array}\)
1.4. Đạo hàm của hàm số mũ và hàm số lôgarit
Ta có công thức đạo hàm của các hàm số mũ và hàm số lôgarit sau:
\(\begin{array}{l} \left( {{e^x}} \right)’ = {e^x}, \text{với mọi }x \in R \\ \left( {{a^x}} \right)’ = {a^x}\ln a,\,\text{với mọi }0 < a \ne 1,\,x \in R \\ \end{array}\)
\(\begin{array}{l} \left( {\ln x} \right)’ = \frac{1}{x} \text{với mọi } x\in (0;+\infty)\\\left( {{{\log }_a}x} \right)’ = \frac{1}{{x\ln a}} \text{với mọi } x\in (0;+\infty) \\ \end{array}\)
1.5. Đạo hàm của tổng, hiệu, tích, thương của hai hàm số
Cho hai hàm số \(u = u\left( x \right)\) và \(v = v\left( x \right)\) có đạo hàm tại điểm x thuộc khoảng xác định. Ta có:
+ \({\left( {u + v} \right)’} = {u’} + {v’}\)
+ \({\left( {u – v} \right)’} = {u’} – {v’}\)
+ \({\left( {u.v} \right)’} = {u’}.v + u.{v’}\) (1)
+ \(\left ( \frac{u}{v} \right )’=\frac{u’v-uv’}{v^2},(v(x) \ne 0)\) (2)
Chú ý: Nếu u = C là một hằng số thì công thức (1) trở thành: \((Cv)’=Cv’.\)
Nếu u = 1 thì công thức (2) trở thành: \({\left( {\frac{1}{v}} \right)’} = – \frac{{ – v’}}{{{v^2}}}\) , \((v(x)\ne 0)\)
1.6. Đạo hàm của hàm hợp
Hàm số y=f(g(x)) được gọi là hàm hợp của hàm số y=f(u) với u=g(x).
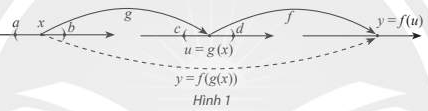
Nếu hàm số u = g(x) có đạo hàm \(u’_x\) tại x và hàm số y = f(u) có đạo hàm \(y’_u\) tại u thì hàm hợp y = f(g(x)) có đạo hàm \(y’_x\) tại x là
1.7. Đạo hàm cấp hai
Hàm số \(y=f(x)\) có đạo hàm tại \(x \in (a;b).\)
– Nếu hàm số \(y’=f'(x)\) có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số \(y=f(x)\) tại x.
– Kí hiệu: \(y”\) hoặc \(f”(x).\)
Ý nghĩa cơ học của đạo hàm cấp hai
– Đạo hàm cấp hai \(f”(t)\) là gia tốc tức thời của chuyển động có phương trình \(s=f(t)\) tại thời điểm t.