1.1. Số liệu ghép nhóm
Mẫu số liệu ghép nhóm thường được trình bày dưới dạng bảng thống kê có dạng như sau:
Bảng 1: Bảng tần số ghép nhóm
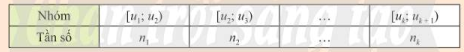
Chú ý:
+ Bảng trên gồm 4 nhóm [uj ; uj + 1) với 1 \(\le\)j\(\le\)k, mỗi nhóm gồm một số giá trị được ghép theo một tiêu chí xác định.
+ Cỡ mẫu \(n = {m_1} + {m_2} + … + {m_k}\).
+ Giá trị chính giữa mỗi nhóm được dùng làm giá trị đại diện cho nhóm ấy. Ví dụ nhóm [u1 ; u2) có giá trị đại diện là \(\frac{{{u_1} + {u_{2}}}}{2}\).
+ Hiệu uj + 1 – uj được gọi là độ dài của nhóm [uj ; uj + 1).
Một số quy tắc ghép nhóm của mẫu số liệu
Mỗi mẫu số liệu có thể được ghép nhóm theo nhiều cách khác nhau nhưng thường tuân theo một số quy tắc sau.
– Sử dụng từ k = 5 đến k = 20 nhóm. Cỡ mẫu càng lớn thì cẩn càng nhiều nhóm số liệu. Các nhóm có cùng độ dài bằng L thoả mãn R < k . L, trong đó R là khoảng biến thiên, k là số nhóm.
– Giá trị nhỏ nhất của mẫu thuộc vào nhóm [u1 ; u2) và càng gần u1 càng tốt. Giá trị lớn nhất của mẫu thuộc nhóm [uk ; uk + 1) và càng gần uk + 1 càng tốt.
1.2. Số trung bình
Giả sử mẫu số liệu được cho dưới dạng băng tần số ghép nhóm

Số trung bình của mẫu số liệu ghép nhóm kí hiệu là \(\overline{x}\) và được tính bởi công thức sau:
|
\[\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + … + {n_k}{c_k}}}{n}\] |
trong đó \(n = {n_1} + {n_2} + … + {n_k}\).
Ý nghĩa của số trung bình của mẫu số liệu ghép nhóm
Số trung bình của mẫu số liệu ghép nhóm là giá trị xấp xỉ cho số trung bình của mẫu số liệu gốc. Nó thường dùng để đo xu thế trung tâm của mẫu số liệu.
1.3. Mốt
Nhóm chứa mốt của mẫu số liệu ghép nhóm là nhóm có tần số lớn nhất.
Giả sử nhóm chứa mốt là [um ; um + 1), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là Mo, được xác định bởi công thức
|
\({M_o} = {a_j} + \frac{{{n_m} – {n_{m – 1}}}}{{\left( {{n_m} – {n_{m – 1}}} \right) + \left( {{n_m} – {n_{m + 1}}} \right)}}.(u_{m + 1}-u_{m}).\) |
Chú ý: Nếu không có nhóm kề trước của nhóm chứa mốt thì \(n_{m – 1}\) = 0. Nếu không có nhóm kể sau của nhóm chứa mốt thì \(n_{m + 1}\) = 0.
Ý nghĩa của mốt của mẫu số liệu ghép nhóm
– Mốt của mẫu số liệu không ghép nhóm là giá trị có khả năng xuất hiện cao nhất khi lấy mẫu Mốt của mẫu số liệu sau khi ghép nhóm Mo, xấp xỉ với mốt của mẫu số liệu không ghép nhóm. Các giá trị nằm xung quanh Mo thường có khả năng xuất hiện cao hơn các giá trị khác.
– Một mẫu số liệu ghép nhóm có thể có nhiều nhóm chứa mốt và nhiều mốt.