Bài toán tìm vận tốc tức thời

– Từ vị trí O, thả viên bi rơi tự do xuống đất và nghiên cứu chuyển động của viên bi. Chọn trục Oy theo phương thẳng đứng, chiều dương hướng xuống đất, gốc O là vị trí ban đầu của viên bi tại thời điểm 0s, và bỏ qua sức cản không khí, ta được phương trình chuyển động của viên bi là y = f(x) =\(1 \over 2\)gx² (g là gia tốc rơi tự do, g \(\approx \) 9,8 m/s²).

 

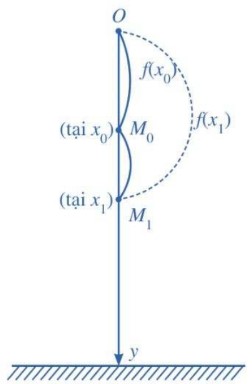
– Giả sử tại thời điểm x₀, viên bi ở vị trí M₀ có y₀ = f(x₀); tại thời điểm x₁ viên bi ở vị trí M₁ có y₁ = f(x₁). Khoảng thời gian từ x0 đến x₁ quãng đường viên bị đi được là M0.M1 = f(x1) – f(x0). Vậy vận tốc trung bình của viên bi trong khoảng thời gian đó là

\( \frac{{f\left( {x_1}\right) – f\left( {{x_0}} \right)}}{{{x_1}- {x_0}}}\)

– Nếu x1 − x0 càng nhỏ thì tỉ số trên càng phản ánh chính xác hơn sự nhanh chậm của viên bi tại thời điểm x0 . Từ đó, người ta xem giới hạn của tỉ số \(\frac{{f\left( {x_1}\right) – f\left( {{x_0}} \right)}}{{{x_1}- {x_0}}}\) khi x1 dần đến x0 là vận tốc tức thời tại thời điểm x0 của viên bị, kí hiệu là v(x0). Nói cách khác:

\(v({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( {x_1} \right) – f\left( {{x_0}} \right)}}{{{x_1} – {x_0}}}\)

– Giá trị \(v({x_0}) \) gọi là đạo hàm của hàm số y = f(x) =\(1 \over 2\)gx2 tại điểm \({x_0}\).

 

Bài toán tìm cường độ tức thời

– Điện lượng Q truyền trong dây dẫn là một hàm số của thời gian t, Q = Q(t). Cường độ trung bình trong khoảng thời gian \(|t − {t_0}|\)  được xác định bởi công thức:

\( \frac{{Q\left( t \right) – Q\left( {{t_0}} \right)}}{{t – {t_0}}}\)

– Nếu \(|t − {t_0}|\) càng nhỏ thì tỉ số này càng biểu thị chính xác hơn cường độ dòng điện tại thời điểm \({t_0}\). Người ta đưa ra định nghĩa sau đây:

– Giới hạn hữu hạn (nếu có) \( \mathop {\lim }\limits_{t \to {t_0}} \frac{{Q\left( t \right) – Q\left( {{t_0}} \right)}}{{t – {t_0}}}\) được gọi là cường độ tức thời của dòng điện tại thời điểm \({t_0}\).

 

– Cho hàm số \(y=f(x)\) xác định trên khoảng (a ; b) và điểm \({{x}_{0}}\in (a;b)\).  – Nếu tồn tại giới hạn hữu hạn \(\underset{x\to {{x}_{0}}}{\mathop{\lim }}\,\frac{f(x)-f({{x}_{0}})}{x-{{x}_{0}}}\) thì giới hạn đó được gọi là đạo hàm của hàm số \(y=f(x)\) tại \({x_0}\) và được kí hiệu là \(f'({{x}_{0}})\) hoặc \(y{{‘}_{{{x}_{0}}}}\)

 

Nhận xét: Trong định nghĩa trên, ta đặt:

– \(\Delta x=x-{{x}_{0}}\) và gọi \(\Delta x\) là số gia của biến số tại điểm \({x_0}\).

– \(\Delta y=f({{x}_{0}}+\Delta x)-f({{x}_{0}})\) và gọi \(\Delta y\) là số gia của hàm số ứng với số gia \(\Delta x\) tại điểm \({x_0}\). Khi đó, ta có:

\(f'({{x}_{0}})=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f({{x}_{0}}+\Delta x)-f({{x}_{0}})}{\Delta x}=\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}\)

 

Cho hàm số \(y=f(x)\) xác định trên khoảng (a ; b) và điểm \({{x}_{0}}\in (a;b)\).

Để tính đạo hàm \(f'({{x}_{0}})\) của hàm số \(y=f(x)\) tại \({x_0}\), ta lần lượt thực hiện:

– Bước 1. Xét \(\Delta x\) là số gia của biến số tại điểm \({x_0}\). Tính \(\Delta y=f({{x}_{0}}+\Delta x)-f({{x}_{0}})\).  – Bước 2. Rút gọn tỉ số \(\frac{\Delta y}{\Delta x}\).  – Bước 3. Tính \(\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}\)  Kết luận: Nếu \(\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{\Delta y}{\Delta x}=a\) thì \(f'({{x}_{0}})=a\).

– Đạo hàm xuất hiện trong nhiều khái niệm vật lí.

– Chẳng hạn: Xét chuyển động thẳng xác định bởi phương trình s = s(t), với s = s(t) là một hàm số có đạo hàm. Như đã thấy trong bài toán mở đầu, vận tốc tức thời của chuyển động tại thời điểm \({t_0}\) là đạo hàm của hàm số tại \({t_0}\): \(v({t_0}) = s'({t_0})\).

 

– Đạo hàm của hàm số y = f(x) tại điểm \({x_0}\) là hệ số góc của tiếp tuyến của đồ thị hàm số đó tại điểm \({{M}_{0}}({{x}_{0}};f({{x}_{0}}))\).  – Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm \({{M}_{0}}({{x}_{0}};f({{x}_{0}}))\) là \(y=f'({{x}_{0}})(x-{{x}_{0}})+f({{x}_{0}})\).