Nhận xét:

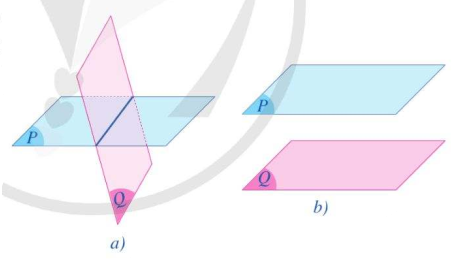
Đối với hai mặt phẳng phân biệt (P) và (Q) trong không gian, có hai khả năng xảy ra:

– Hai mặt phẳng (P) và (Q) có điểm chung. Khi đó, chúng cắt nhau theo một đường thẳng (Hình a).

– Hai mặt phẳng (P) và (Q) không có điểm chung. Khi đó, ta nói chúng song song với nhau, kí hiệu (P) // (Q) hay (Q) // (P) (Hình b).

 

 

Hai mặt phẳng được gọi là song song với nhau nếu chúng không có điểm chung.

 

Định lí 1: (Dấu hiệu nhận biết hai mặt phẳng song song)

Nếu mặt phẳng (P) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (Q) thì (P) song song với (Q).

 

Định lí 2: (Tính chất về hai mặt phẳng song song)

Qua một điểm nằm ngoài một mặt phẳng cho trước, có một và chỉ một mặt phẳng song song với mặt phẳng đã cho.

– Tức là, cho điểm M nằm ngoài mặt phẳng (Q), có duy nhất một mặt phẳng (P) chứa điểm M và song song với mặt phẳng (Q).

 

Từ định lí trên, ta có các hệ quả sau:

– Hệ quả 1. Nếu đường thẳng a song song với mặt phẳng (Q) thì có duy nhất một mặt phẳng (P) chứa a và song song với mặt phẳng (Q).

– Hệ quả 2. Hai mặt phẳng phân biệt cùng song song với mặt phẳng thứ ba thì song song với nhau.

 

Định lí 3: 

Cho hai mặt phẳng song song (P) và (Q). Nếu mặt phẳng (R) cắt mặt phẳng (P) thì cũng cắt mặt phẳng (Q) và hai giao tuyến a, b của chúng song song với nhau.

 

Định lí 4: (Định lí Thalès)

Nếu a, b là hai đường thẳng phân biệt cắt ba mặt phẳng song song (P), (Q), (R) lần lượt tại các điểm A, B, C và A’, B’, C’ thì: \(\frac{AB}{A’B’}=\frac{BC}{B’C’}=\frac{CA}{C’A’}\)