– Đường thẳng đi qua điểm đầu và điểm cuối của một vectơ được gọi là giá của vectơ đó.

– Hai vectơ được gọi là cùng phương nếu chúng có giá song song hoặc trùng nhau.

– Đối với hai vectơ cùng phương thì chúng cùng hướng hoặc ngược hướng.

– Hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\) được gọi là bằng nhau, kí hiệu \(\overrightarrow a  = \overrightarrow b \), nếu chúng có cùng độ dài và cùng hướng.

a) Tổng của hai vectơ

– Cho hai vectơ \(\overrightarrow a ,\overrightarrow b \). Lấy một điểm A tuỳ ý và vẽ \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {BC}  = \overrightarrow b \) (Hình bên dưới). Khi đó vectơ \(\overrightarrow {AC} \) được gọi là tổng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  + \overrightarrow b \). 

– Phép lấy tổng của hai vectơ được gọi là phép cộng vectơ.

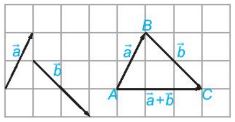
– Quy tắc ba điểm: Với ba điểm bắt kì A, B, C, ta có \(\overrightarrow {AB}  + \overrightarrow {BC}  = \overrightarrow {AC} \)

– Quy tắc hình bình hành: Nếu ABCD là một hình binh hành thì \(\overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC} \) 

– Với ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) tuỳ ý:

• Tính chất giao hoán: \(\overrightarrow a  + \overrightarrow b  = \overrightarrow b  + \overrightarrow a \)

• Tính chất kết hợp: \(\left( {\overrightarrow a  + \overrightarrow b } \right) + \overrightarrow c  = \overrightarrow a  + \left( {\overrightarrow b  + \overrightarrow c } \right)\)

• Tính chất của vectơ-không: \(\overrightarrow a  + \overrightarrow 0  = \overrightarrow 0  + \overrightarrow a  = \overrightarrow a \) 

b) Hiệu của hai vectơ

– Vectơ có cùng độ dài và ngược hướng với vectơ \(\overrightarrow a \) được gọi là vectơ đối của vectơ \(\overrightarrow a \). Vectơ đối của \(\overrightarrow a \) được kí hiệu là \(-\overrightarrow a \).

– Vectơ \(\overrightarrow 0 \) được coi là vectơ đối của chính nó.

– Vectơ \(\overrightarrow a  + \left( { – \overrightarrow b } \right)\) được gọi là hiệu của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) và được kí hiệu là \(\overrightarrow a  – \overrightarrow b \). Phép lấy hiệu hai vectơ được gọi là phép trừ vectơ.

– Quy tắc hiệu: Với ba điểm O, M, N, ta có \(\overrightarrow {MN}  = \overrightarrow {ON}  – \overrightarrow {OM} \)

Tích của một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) với một số thực k > 0 là một vectơ, ki hiệu là \(k\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a\) và có độ dài bằng \(k\left| {\overrightarrow a } \right|\).

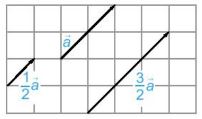
Tích của một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) với một số thực k <0 là một vectơ, ki hiệu là \(k\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a\) và có độ dài bằng \(-k\left| {\overrightarrow a } \right|\).

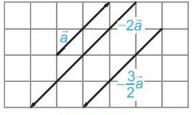
– Các tính chất của phép nhân vectơ với một số

Với hai vectơ \(\overrightarrow a ,\overrightarrow b\) và hai số thực k, t, ta luôn có: 

\(\begin{array}{l}
*k\left( {t\overrightarrow a } \right) = \left( {kt} \right)\overrightarrow a \\
*\left( {k + t} \right)\overrightarrow a  = k\overrightarrow a  + t\overrightarrow a \\
*k\left( {\overrightarrow a  + \overrightarrow b } \right) = k\overrightarrow a  + k\overrightarrow b ;\left( {\overrightarrow a  – \overrightarrow b } \right) = k\overrightarrow a  – k\overrightarrow b .\\
*1\overrightarrow a  = \overrightarrow a ;\left( { – 1} \right)\overrightarrow a  =  – \overrightarrow a 
\end{array}\)

a) Tọa độ của vectơ

Với mỗi vectơ ứ trên mặt phẳng Oxy, có duy nhất cặp số \(\left( {{x_0};{y_0}} \right)\) sao cho \(\overrightarrow u  = {x_0}\overrightarrow i  + {y_0}\overrightarrow j \). Ta nói vectơ \(\overrightarrow u \) có toạ độ \(\left( {{x_0};{y_0}} \right)\) và viết \(\overrightarrow u  = \left( {{x_0};{y_0}} \right)\) hay \(\overrightarrow u \left( {{x_0};{y_0}} \right)\). Các số \({{x_0},{y_0}}\) tương ứng được gọi là hoành độ, tung độ của \(\overrightarrow u \).

b) Biểu thức tọa độ của các phép toán vectơ

– Cho hai vectơ \(\overrightarrow u  = \left( {x;y} \right)\) và \(\overrightarrow v  = \left( {x;y} \right)\). Khi đó:

\(\begin{array}{*{20}{l}}
{*\vec u + \vec v = \left( {x + x’;y + y’} \right);}\\
{*\vec u – \vec v = \left( {x – x’;y – y’} \right);}\\
{*k\vec u = \left( {kx;ky} \right),k \in R}
\end{array}\)

– Nếu điểm M có toạ độ (x; y) thì vecto \(\overrightarrow {OM} \) có toạ độ (x; y) và độ dài \(\left| {\overrightarrow {OM} } \right| = \sqrt {{x^2} + {y^2}} \).

– Với hai điểm M(x; y) và N(x’; y’) thì \(\overrightarrow {MN}  = \left( {x’ – x;y’ – y} \right)\) và khoảng cách giữa hai điểm M, N là \(\left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( {x’ – x} \right)}^2} + {{\left( {y’ – y} \right)}^2}} \) 

a) Góc giữa hai vectơ

Cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) khác \({\vec 0}\). Từ một điểm A tuỳ ý, vẽ các vectơ \(\overrightarrow {AB}  = \overrightarrow u \) và \(\overrightarrow {AC}  = \overrightarrow v \) (Hình cho bên dưới). Khi đó, số đo của góc BAC được gọi là số đo góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) hay đơn giản là góc giữa hai vectơ \(\overrightarrow u \), \(\overrightarrow v \) kí hiệu là \(\left( {\overrightarrow u ,\overrightarrow v } \right)\).

b) Tích vô hướng của hai vectơ

Tích vô hướng của hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) là một số, kí hiệu là \(\overrightarrow u .\overrightarrow v \), được xác định bởi công thức sau:

\(\overrightarrow u .\overrightarrow v  = \left| {\overrightarrow u } \right|.\left| {\overrightarrow v } \right|.cos\left( {\overrightarrow u ,\overrightarrow v } \right)\) 

c) Biểu thức tọa độ và tính chất của tích vô hướng

Tích vô hướng của hai vectơ \(\overrightarrow u  = \left( {x’;y’} \right)\) được tính theo công thức: \(\overrightarrow u .\overrightarrow v  = xx’ + yy’\)

Tính chất của tích vô hướng 

Với ba vectơ \(\overrightarrow u ,\overrightarrow v ,\overrightarrow {\rm{w}} \) bất kì và mọi số thực k. ta có:

* \(\overrightarrow u .\overrightarrow v  = \overrightarrow v .\overrightarrow u \) (tính chất giao hoán);

* \(\overrightarrow u .\left( {\overrightarrow v  + \overrightarrow {\rm{w}} } \right) = \overrightarrow u .\overrightarrow v  + \overrightarrow u .\overrightarrow {\rm{w}} \) (tính chất phân phối đối với phép cộng);

* \(\left( {k\overrightarrow u } \right).\overrightarrow v  = k\left( {\overrightarrow u .\overrightarrow v } \right) = \overrightarrow u \left( {k.\overrightarrow v } \right)\).