a) Mệnh đề, mệnh đề chứa biến

– Mỗi mệnh đề phải hoặc đúng hoặc sai.

– Một mệnh đề không thể vừa đúng vửa sai.

b) Mệnh đề phủ định

Mệnh đề P và mệnh đề \(\overline P\) là hai mệnh đề trái ngược nhau. Nếu P đúng thì \(\overline P\) sai, còn nếu P sai thì \(\overline P\) đúng

c) Mệnh đề kéo theo, mệnh đề đảo

– Mệnh đề “Nếu P thì Q” được gọi là một mệnh đề kéo theo và kí hiệu là P=> Q

– P là giả thuyết của định lí, Q là kết luận của định lí, hoặc ” P là điều kiện đủ để có Q” hoặc “Q là điều kiện cần để có P”. 

– Mệnh đề Q => P được gọi là mệnh đề đảo của mệnh đề P => Q

Nhận xét: 

– Mệnh đề đảo của một mệnh đề đúng không nhất thiết là đúng. 

– Nếu cả hai mệnh đề P => Q và Q => P đều đúng thì mệnh đề tương đương \(P \Leftrightarrow Q\) đúng. Khi đó, ta nói “P tương đương với Q” hoặc “P là điều kiện cần và đủ để có Q” hoặc “P khi và chỉ khi Q”.

– Câu “Mọi số thực đều có bình phương không âm” là một mệnh đề. Có thể viết mệnh đề này như sau: \(P:\forall x \in R,{x^2} \ge 0\) 

– Câu “Có một số hữu tỉ mà bình phương của nó bằng 2” là một mệnh đề. Có thể viết mệnh đề này như sau: \(Q:\exists x \in Q,{x^2} = 2\)

Kí hiệu \(\forall\) đọc là “với mọi” Kí hiệu \(\exists\) đọc là “tồn tại”

a) Tập hợp

*Có thể mô tả một tập hợp bằng một trong hai cách sau:

– Cách 1: Liệt kê các phần tử của tâp hợp;

– Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp.

a \( \in \) S phần tử a thuộc tập hợp S. a \( \notin \) S phần tử a không thuộc tập hợp S.

Chú ý: Số phần tử của tập hợp S được kí hiệu là n(S). 

* Tập hợp không chưa phần tử nào được goin là tập rộng, kí hiệu là \(\emptyset \)

Chẳng hạn:

– Tập hợp các nghiệm của phương trình x2 + 1 = 0 là tập rộng;

– Tập hợp những người sống trên Mặt Trời là tập rỗng.

b) Tập hợp con

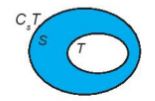
– Nếu mọi phần tử của tập hợp T đều là phần tử của tập hợp S thì ta nói T là một tập hợp con (tập con) của S và viết là \(T \subset S\) (đọc là T chứ trong S hoặc T là tập hợp con của S).

• Thay cho \(T \subset S\), ta còn viết \(S \supset T\) (đọc là S chứa T).
• Kí hiệu \(T \not\subset S\) để chỉ T không lả tập con của S.

Nhận xét:

• Từ định nghĩa trên, T là tập con của S nếu mệnh đề sau đúng: \(\forall x,x \in T \Rightarrow x \in S\).
• Quy ước tập rộng là tập con của mọi tập hợp.

c) Hai tập hợp bằng nhau

Hai tập hợp S và T được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần tử của tập hợp S và ngược lại. Kí hiệu S = T

a) Mối quan hệ giữa các tập hợp số

– Tập hợp các số tự nhiên N = {0; 1; 2; 3; 4; …}

– Tập hợp các số nguyênZ gồm các số tự nhiên và các số nguyên âm: Z = {…; -3; -2; -1; 0; 1; 2; 3;…}

– Tập hợp các số hữu tỉ Q gồm các số viết được dưới dạng phân số \(\frac{a}{b}\), với a, b \(\in\) Z, b \( \ne \) 0. Số hữu tỉ còn được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn.

– tập hợp các số thực R gồm các số hữu tỉ. Số vô tỉ là các số thập phân vô hạn không tuần hoàn. 

Mối quan hệ giữa các tập hợp số: \(N \subset Z \subset Q \subset R\) 

b) Các tập con thường dùng của \(\mathbb{R}\)

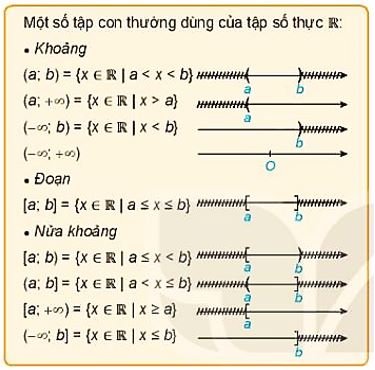
– Kí hiệu \( + \infty \): Đọc là dương vô cực (hoặc dương vô cùng).

– Kí hiệu \( – \infty \): Đọc là âm vô cực (hoặc âm vô cùng).

– a, b gọi là các đầu mút của đoạn, khoảng hay nửa khoảng. 

c) Các phép toán trên tập hợp

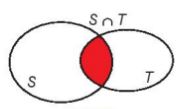
– Tập hợp các phần tử thuộc cả hai tập hợp S và T gọi là giao của hai tập hợp S và T, kí hiệu là \(S \cap T\).

\(S \cap T = \{ x|x \in S\) và \(x \in T\} \). 

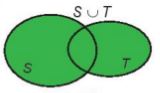
– Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp T gọi là hợp của hai tập hợp S và T, kí hiệu là \(S \cup T\). 

\(S \cup T = \{ x|x \in S\) hoặc \(x \in T\} \)

– Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử thuộc S nhưng không thuộc T, kí hiệu là S\T.

S\T = {x | x\(\in\) S và x \(\notin\) T}.

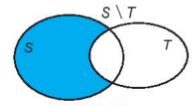
– Nếu \(T \subset S\) thì S\T được gọi là phần bù của T trong S, kí hiệu là CST