Tích của một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) với một số thực k > 0 là một vectơ, ki hiệu là \(k\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a\) và có độ dài bằng \(k\left| {\overrightarrow a } \right|\).

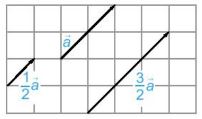
Tích của một vectơ \(\overrightarrow a  \ne \overrightarrow 0 \) với một số thực k <0 là một vectơ, ki hiệu là \(k\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a\) và có độ dài bằng \(-k\left| {\overrightarrow a } \right|\).

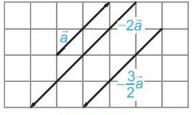
Chú ý: Ta quy ước \(k\overrightarrow a  = \overrightarrow 0 \) nếu \(\overrightarrow a  = \overrightarrow 0 \) hoặc k = 0.

Trong hình cho sau, hai trung tuyến AM và BN của tam giác ABC cắt nhau tại G.

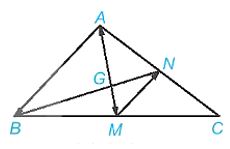
Ta có \(\overrightarrow {GA}  =  – 2\overrightarrow {GM} ,\overrightarrow {MN}  =  – \frac{1}{2}\overrightarrow {AB} \)

Nhận xét: Vectơ \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và cùng hướng với \(\overrightarrow a \) nếu \(k \ge 0\), ngược hướng với \(\overrightarrow a \) nếu \(\overrightarrow a  \ne \overrightarrow 0 \) và k < 0.

Ví dụ: Chứng minh rằng hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) (\(\overrightarrow b  \ne \overrightarrow 0 \)) cùng phương khi và chỉ khi tồn tại số k để \(\overrightarrow a  = k\overrightarrow b \). 

Giải

Thật vậy, nếu \(\overrightarrow a  = k\overrightarrow b \) thi \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương. Ngược lại, giả sử \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương.

Ta lấy \(k = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}\) nếu \(\overrightarrow a \) và \(\overrightarrow b \) cùng hướng và lấy \(k = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}\) nếu \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng.

Khi đó \(\overrightarrow a  = k\overrightarrow b \).

Với hai vectơ \(\overrightarrow a ,\overrightarrow b\) và hai số thực k, t, ta luôn có:  \(\begin{array}{l} *k\left( {t\overrightarrow a } \right) = \left( {kt} \right)\overrightarrow a \\ *\left( {k + t} \right)\overrightarrow a  = k\overrightarrow a  + t\overrightarrow a \\ *k\left( {\overrightarrow a  + \overrightarrow b } \right) = k\overrightarrow a  + k\overrightarrow b ;\left( {\overrightarrow a  – \overrightarrow b } \right) = k\overrightarrow a  – k\overrightarrow b .\\ *1\overrightarrow a  = \overrightarrow a ;\left( { – 1} \right)\overrightarrow a  =  – \overrightarrow a  \end{array}\)

Nhận xét: 

– Điểm I là trung của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 \)

– Điểm G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  = \overrightarrow 0 \)

Chú ý: Cho hai vectơ không cùng phương \(\overrightarrow a ,\overrightarrow b \) (Hình bên dưới). Khi đó, mọi vectơ \(\overrightarrow u \) đều biểu thị (phân tích) được một cách duy nhất theo hai vectơ \(\overrightarrow a ,\overrightarrow b \) nghĩa là có duy nhất cặp số (x;y) sao cho \(\overrightarrow u  = x\overrightarrow a  + y\overrightarrow b \). 

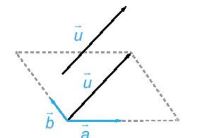
Ví dụ: Cho đoạn thẳng AB có trung điểm I. Chứng minh rằng với điểm O tuỳ ý, ta có \(\overrightarrow {OA}  + \overrightarrow {OB}  = 2\overrightarrow {OI} \)

Giải

Vì I là trung điểm của AB nên \(\overrightarrow {IA}  + \overrightarrow {IB}  = \overrightarrow 0 \) 

Do đó \(\overrightarrow {OA}  + \overrightarrow {OB}  = \left( {\overrightarrow {OI}  + \overrightarrow {IA} } \right) + \left( {\overrightarrow {OI}  + \overrightarrow {IB} } \right) = 2\overrightarrow {OI}  + \left( {\overrightarrow {IA}  + \overrightarrow {IB} } \right) = 2\overrightarrow {OI} \)