Định lí côsin. Trong tam giác ABC: \(\begin{array}{l} {a^2} = {b^2} + {c^2} – 2bc\cos A,\\ {b^2} = {c^2} + {a^2} – 2ca\cos B,\\ {c^2} = {a^2} + {b^2} – 2ab\cos C. \end{array}\)

Ví dụ: Cho tam giác ABC có \(\widehat A = {120^0}\) và AB = 5, AC = 8. Tính độ dài cạnh BC.

Giải

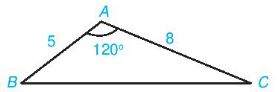
Áp dụng định lí côsin cho tam giác ABC, ta có:

\(\begin{array}{l}
B{C^2} = A{B^2} + A{C^2} – 2AB.AC.cos{120^0}\\
 = {5^2} + {8^2} – 2.5.8.\left( { – \frac{1}{2} = 129} \right)
\end{array}\)

Vậy \(BC = \sqrt {129} \)

Định lí sin. Trong tam giác ABC: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

Ví dụ: Cho tam giác ABC có \(\widehat A = {135^0},\widehat C = {15^0}\) và b = 12. Tính a, c, R và số đo góc B.

Giải

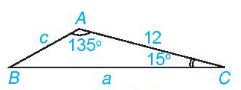
Ta có: \(\widehat B = {180^0} – \left( {\widehat A + \widehat C} \right) = {180^0} – \left( {{{135}^0} + {{15}^0}} \right) = {30^0}\)

Áp dụng định lí sin, ta có: \(\frac{a}{{\sin {{135}^0}}} = \frac{{12}}{{\sin {{30}^0}}} = \frac{c}{{\sin {{15}^0}}} = 2R\) 

Suy ra:

\(\begin{array}{l}
a = \frac{{12}}{{\sin {{30}^0}}}.\sin {135^0} = 12\sqrt {12} ;\\
c = \frac{{12}}{{\sin {{30}^0}}}.\sin {15^0} = 24\sin {15^0}\left( { \approx 6,21} \right);\\
R = \frac{{12}}{{2\sin {{30}^0}}} = 12
\end{array}\)

Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một sô yêu tô của tam giác đó được gọi là giải tam giác.

Ví dụ: Giải tam giác ABC, biết \(c = 14,\widehat A = {60^0},\widehat B = {40^0}\).

Giải

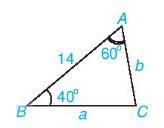
Ta có: \(\widehat C = {180^0} – \left( {\widehat A + \widehat B} \right) = {80^0}\)

Áp dụng định lí sin, ta có: \(\frac{a}{{\sin {{60}^0}}} = \frac{b}{{\sin {{40}^0}}} = \frac{{14}}{{\sin {{80}^0}}}\) 

Suy ra: \(a = \frac{{14\sin {{60}^0}}}{{\sin {{80}^0}}} \approx 12,31;b = \frac{{14\sin {{40}^0}}}{{\sin {{80}^0}}} \approx 9,14\)

Chú ý: Áp dụng các định li côsin, sin và sử dụng máy tính cằm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:

• Biết hai cạnh và góc xen giữa;
• Biết ba cạnh;
• Biết một cạnh và hai góc kề.

Công thức tính diện tích tam giác ABC:   \(\begin{array}{l} *S = pr = \frac{{\left( {a + b + c} \right)r}}{2}\\ *S = \frac{1}{2}bc\sin A = \frac{1}{2}casinB = \frac{1}{2}ab\sin C\\ *S = \frac{{abc}}{{4R}}\\ *\sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)}  \end{array}\)

Ví dụ: Cho tam giác ABC có a = 13, b = 14, c = 15.

a) Tính sinA.

b) Tính diện tích S bằng hai cách khác nhau.

Giải

a) Áp dụng định lí côsin, ta có: \(\cos A = \frac{{{b^2} + {c^2} – {a^2}}}{{2bc}} = \frac{{{{14}^2} + 15 – {{13}^2}}}{{420}} = 0,6\) 

Do đó \(\sin A = \sqrt {1 – co{s^2}A}  = 0,8\) 

b) Ta có \(S = \frac{1}{2}bc\sin A = 84\).

Áp dụng công thức Heron, ta cũng có thể tính S theo cách thứ hai như sau:

Tam giác ABC có nửa chu vi là: \(p = \frac{{a + b + c}}{2} = \frac{{13 + 14 + 15}}{2} = 21\) 

Khi đó \({S_{ABC}} = \sqrt {p(p – a)(p – b)(p – c)}  = \sqrt {21.(21 – 13).(21 – 14).(21 – 15)}  = \sqrt {21.8.7.6}  = 84\)