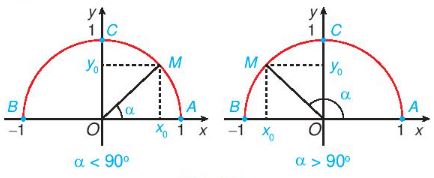
Trong mặt phẳng toạ độ Oxy, nửa đường tròn tâm O, bán kính R = 1 nằm phía trên trục hoành (Hình cho sau) được gọi là nửa đường tròn đơn vị.

Cho trước một góc \(\alpha\), \(0^\circ  \le \alpha  \le 180^\circ \). Khi đó, có duy nhất điểm M(x₀; y₀) trên nửa đường tròn đơn vị nói trên đề \(\widehat {xOM} = \alpha \). 

Ta có các công thức sau:

\(\tan \alpha  = \frac{{\sin \alpha }}{{cos\alpha }}(\alpha  \ne {90^0});\cot \alpha  = \frac{{cos\alpha }}{{\sin \alpha }}(\alpha  \ne {0^0}\) và \(\alpha  \ne {180^0});\) \(\tan \alpha  = \frac{1}{{\cot \alpha }}\left( {\alpha  \notin \left\{ {{0^0};{{90}^0};{{180}^0}} \right\}} \right)\)

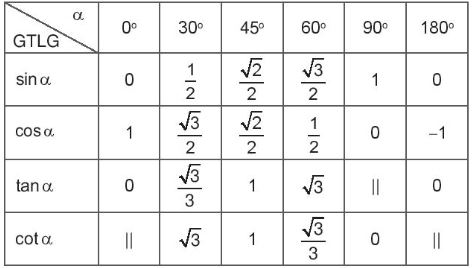
Sau đây là bảng giá trị lượng giác (GTLG) của một số góc đặc biệt mà em nên nhớ.

Chú ý

– Khi tìm x biết sin x, máy tính chỉ đưa ra giá trị \(x \le {90^0}\).

– Muốn tìm x khi biết cos x, tan x, ta cũng làm tương tự như trên, chỉ thay phím sin tương  ứng bởi phim cos , tan.

Ví dụ: Tìm các giá trị lượng giác của góc 135°.

Giải 

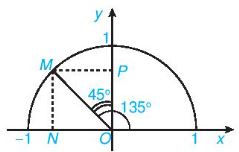
Gọi M là điểm trên nửa đường tròn đơn vị sao cho \(\widehat {xOM} = 135^\circ \). Gọi N, P tương ứng là hình chiếu vuông góc của M lên các trục Ox, Oy.

Vì \(\widehat {xOM} = 135^\circ \) nên \(\widehat {MON} = 45^\circ \), \(\widehat {MOP} = 45^\circ \). Vậy các tam giác MON, MOP là vuông cân với cạnh huyền OM= 1.

Từ đó, ta có \(ON = OP = \frac{{\sqrt 2 }}{2}\) Mặt khác, điểm M nằm bên trái trục tung nên có toạ độ là \(\left( { – \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\). 

Theo định nghĩa, ta có:

\(\begin{array}{l}
\sin {135^0} = \frac{{\sqrt 2 }}{2};\;\;\;\;\;\;\;\;\;cos{135^0} =  – \frac{{\sqrt 2 }}{2};\\
\tan {135^0} =  – 1;\;\;\;\;\;\;\;\;\;\;\cot {135^0} =  – 1
\end{array}\)

Ở lớp 9, em đã biết mối quan hệ giữa tỉ số lượng giác của hai góc phụ nhau. Trong mục này, em hãy tìm mối quan hệ giữa các giá trị lượng giác của hai góc bù nhau.

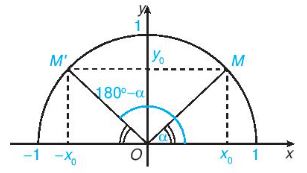
Đối với một góc \(\alpha\) tuỳ ý \({0^0} \le \alpha  \le {180^0}\), gọi M, M’ là hai điểm trên nửa đường tròn đơn vị tương ứng với hai góc bù nhau \(\alpha\) và \({180^0} – \alpha \) \(\left( {\widehat {xOM} = \alpha ,\widehat {xOM’} = {{180}^0} – \alpha } \right)\)

Đối với hai góc bù nhau, \(\alpha \) và \({{{180}^0} – \alpha }\), ta có: \(\begin{array}{l} *\sin \left( {{{180}^0} – \alpha } \right) = \sin \alpha ;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;*cos\left( {{{180}^0} – \alpha } \right) =  – cos\alpha \\ *\tan \left( {{{180}^0} – \alpha } \right) =  – \tan \left( {x \ne {{90}^0}} \right);\;\;\;\;\;\;\;\;\;*\cot \left( {{{180}^0} – \alpha } \right) =  – \cot \alpha \left( {{0^0} < \alpha  < {{180}^0}} \right) \end{array}\)

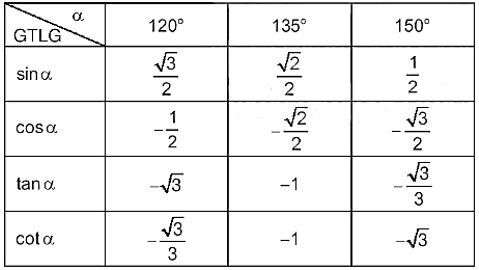
Ví dụ: Tính các giá trị lượng giác của các góc 120°,135°,150°.

Giải

Do các góc 120°,135°,150° tương ứng bù với các góc 60°,45°,30°, ta cũng có bảng các giá trị lượng giác sau: