Bất phương trình bậc nhất hai ẩn x, y có dạng tổng quát là: \(ax + by \le c\left( {ax + by \ge c,ax + by < c,ax + by > c} \right)\)  (trong đó a, b, c là những số thực đã cho, a và b không đồng thời bằng 0, x và y là các ẩn số.) Cặp số (x0; y0) được gọi là một nghiệm của bất phương trình bậc nhất hai ẩn \(ax + by \le c\) nếu bất đẳng thức \(a{x_0} + b{y_0} \le c\) đúng.

Nhận xét: Bất phương trình bậc nhất hai ẩn luôn có vô số nghiệm.

Ví dụ: Cặp số (x; y) = (100; 100) thoả mãn bất phương trình bậc nhất hai ẩn nào trong hai bất phương trình thu được ở HĐ1? Từ đó cho biết rạp chiếu phim có phải bù lỗ hay không nếu bán được 100 vé loại 1 và 100 vé loại 2.

Trả lời câu hỏi tương tự với cặp số (x; y) = (150; 150).

Giải

Bước 1:

Từ HĐ 1 ta có hai bất phương trình:

\(x + 2y \ge 400\left( 1 \right)\) và \(x + 2y < 400\left( 2 \right)\)

Thay x=100 và y=100 vào bất phương trình (1) ta được:

\(100 + 2.100 \ge 400 \Leftrightarrow 300 \ge 400\) (Vô lí)

=> Cặp số (x;y)=(100;100) không thỏa mãn bất phương trình (1).

Thay x=100 và y=100 vào bất phương trình (2) ta được:

\(100 + 2.100 < 400 \Leftrightarrow 300 < 400\) (Đúng)

=> Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2).

Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2) có nghĩa là nếu bán được 100 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim phải bù lỗ.

Bước 2:

Thay x=150 và y=150 vào bất phương trình (1) ta được:

\(150 + 2.150 \ge 400 \Leftrightarrow 450 \ge 400\) (Đúng)

=> Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1).

Thay x=150 và y=150 vào bất phương trình (2) ta được:

\(150 + 2.150 < 400 \Leftrightarrow 450 < 400\) (Vô lí)

=> Cặp số (x;y)=(150;150) không thỏa mãn bất phương trình (2).

Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1) có nghĩa là nếu bán được 150 vé loại 1 và 150 vé loại 2 thì rạp chiếu phim không phải bù lỗ.

– Trong mặt phẳng toạ độ Oxy, tập hợp các điểm có toạ độ là nghiệm của bất phương trình \(ax + by \le c\) được gọi là miền nghiệm của bất phương trình đó.

– Người ta chứng minh được rằng đường thẳng d có phương trình ax + by = z chia mặt phẳng toạ độ Oxy thành hai nửa mặt phẳng bờ d:

+ Một nửa mặt phẳng (không kể bờ d) gồm các điểm có toạ độ (x; y) thoả mãn ax + by > c;

+ Nửa mặt phẳng còn lại (không kể bờ d) gồm các điểm có toạ độ (x; y) thoả mãn ax + by < c.

(Bờ d gồm các điểm có toạ độ (x; y) thoả mãn ax + by = c.)

– Cách biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn \(ax + by \le c\) 

+ Vẽ đường thẳng d: ax + by = c trên mặt phẳng toạ độ Oxy.

+ Lấy một điểm M₀(x₀; y₀) không thuộc d. 

+ Tính \(a{x_0} + b{y_0}\) và so sánh với c.

+ Nếu \(a{x_0} + b{y_0} < c\) thì nửa mặt phẳng bờ d chứa M₀ là miền nghiệm của bất phương trình. Nếu \(a{x_0} + b{y_0} > c\) thì nửa mặt phẳng bờ d không chứa M0 là miền nghiệm của bất phương trình.

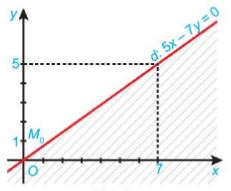
Ví dụ: Biểu diễn miền nghiệm của bất phương trình \(5x{\rm{ }} – {\rm{ }}7y\;{\rm{ }} \le {\rm{ }}0\) trên mặt phẳng toạ độ 

Giải

Bước 1: Vẽ đường thẳng d: 5x – 7y = 0 trên mặt phẳng toạ độ Oxy

Bước 2: Lấy điểm M₀(0; 1) không thuộc d và thay x = 0, y = 1 vào biểu thức 5x – 7y ta được: 5.0 – 7.1 = -7 < 0.

Do đó miền nghiệm của bất phương trình là nửa mặt phẳng bờ d chứa điểm M₀ (miền không bị gạch).

Chú ý: Miền nghiệm của bất phương trình ax + by < c là miền nghiệm của bắt phương trình \(ax + by \le c\) bỏ đi đường thẳng ax + by = c và biểu diễn đường thẳng bằng nét đứt.