Ở lớp 9 ta đã biết những khái niệm quan trọng sau:

+ Phép thử ngấu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà kết quả của nó không thể biết được trước khi phép thử được thực hiện.  + Không gian mẫu của phép thử là tập hợp tất cả các kết quả có thể khi thực hiện phép thử Không gian mẫu của phép thử được kí hiệu là \(\Omega \). + Kết quả thuận lợi cho một biến cố E liên quan tới phép thử T là kết quả của phép thử T làm cho biến cố đó xảy ra.

Chú ý: Ta chỉ xét các phép thử mà không gian mẫu gồm hữu hạn kết quả.

Ví dụ 1: Một tổ trong lớp 10A có ba học sinh nữ là Hương, Hồng, Dung và bồn học sinh nam là Sơn, Tùng, Hoàng, Tiến. Giáo viên chọn ngẫu nhiên một học sinh trong tổ đó để kiểm tra vở bài tập. Phép thử ngẫu nhiên là gỉ? Mô tả không gian mẫu.

Giải

Phép thử ngẫu nhiên là chọn ngẫu nhiên một học sinh trong tổ đẻ kiểm tra vở bài tập.

Không gian mẫu là tập hợp tất cà các học sinh trong tổ.

Ta có \(\Omega \) = (Hương; Hồng: Dung; Sơn; Tùng, Hoàng; Tiến).

* Theo định nghĩa, ta thấy mỗi kết quả thuân lợi cho biến cố E chính là một phần tử thuộc không gian mẫu \(\Omega \). Do đó về mặt toán học, ta có:

Mỗi biến cố là một tập con của không gian mẫu \(\Omega \). Tập con này là tập tất cae các kết quả thuận lợi cho biến cố đó.

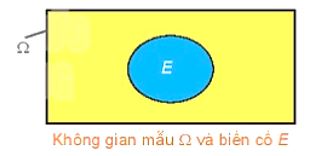
Nhận xét: Biến cố chắc chắn là tập \(\Omega \), biến cố không thể là tập \(\emptyset \). 

Biến cố đối của biến cố E là biến cố “E không xảy ra”. Biến cố đối của E được kí hiệu là \(\overline E \).

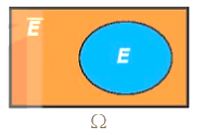
Nhận xét: Nếu biến cố E là tập con của không gian mẫu \(\Omega \) thì biến cố đối \(\overline E \) là tập tất cả các phần tử của \(\Omega \) mà không là phần tử của E. Vậy biến cố \(\overline E \) là phần bù của E trong \(\Omega :\overline E  = {C_\Omega }E\). 

Ví dụ: Gieo một con xúc xắc 6 mặt và quan sát số chấm xuất hiện trên con xúc xắc.

a) Mô tà không gian mẫu.

b) Gọi M là biến cổ: “Số chấm xuất hiện trên con xúc xắc lả một số chẵn”. Nội dung biến cố đối \(\overline M \) của M là gì?

c) Biến cố M và \(\overline M \) là tập con nào của không gian mẫu?

Giải

a) Không gian mẫu \(\Omega \) = {1: 2; 3: 4; 5; 6).

b) Biến cố đối \(\overline M \) của Mà biến có: “Số chấm xuất hiện trên con xúc xắc là một số lẻ”

c) Ta có \(M = \left\{ {2;4;6} \right\} \subset \Omega ;\overline M  = {C_\Omega }M = \left\{ {1;3;5} \right\} \subset \Omega \). 

Ta đã biết không gian mẫu \(\Omega \) của phép thử T là tập hợp tất cả các kết quả có thể của T, biến có E liên quan đến phép thử T là tập con của \(\Omega \). Vì thế số kết quả có thể của phép thử T chính là số phần tử tập \(\Omega \); số kết quả thuận lợi của biến cố E chính là số phản tử của tập E. Do đó, ta có định nghĩa cổ điển của xác suất như sau:

Cho phép thử T có không gian mẫu là \(\Omega \). Giả thiết rằng các kết quả có thể của T là đồng khả năng. Khi đó nếu E là một biến cổ liên quan đến phép thử T thì xác suất của E được cho bởi công thức \(P\left( E \right) = \frac{{n\left( E \right)}}{{n\left( \Omega  \right)}}\).  trong đỏ \({n\left( \Omega  \right)}\) và \({n\left( E \right)}\) tương ứng là số phần tử của tập \(\Omega \) và tập E.

Nhận xét

+ Với mỗi biến cố E, ta có \(0 \le P\left( E \right) \le 1\). 

+ Với biến cố chắc chắn (lả tập \(\Omega \)), ta có P(\(\Omega \)) = 1.

+ Với biến cố không thể (lả tập \(\emptyset \) ), ta có P(\(\emptyset \)) = 0.

Ví dụ: Hai túi I và II chứa các tấm thẻ được đánh số. Túi I: (1; 2; 3; 4; 6}, túi II: {1; 2; 3; 4}. Rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II. Tỉnh xác suất để tổng hai số trên hai tấm thẻ lớn hơn 6.

Giải

Mô tả không gian mẫu \(\Omega \) bằng cách lập bảng như sau.

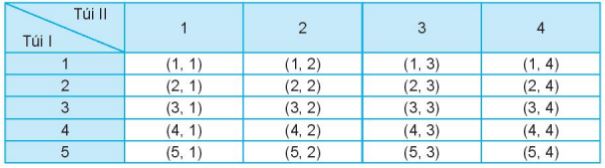
Mỗi ô là một kết quả có thể. Có 20 ô, vậy n(\(\Omega \)) = 20.

Biến cố E: “Tổng hai số trên hai tắm thẻ lớn hơn 6” xảy ra khi tổng là một trong ba trường hợp

Tổng bằng 7 gồm các kết quả: (3, 4); (4, 3); (5. 2).

Tổng bằng 8 gồm các kết quả: (4, 4); (5, 3).

Tổng bằng 9 có một kết quả: (5, 4). 

Vậy biến cố E = ((3, 4); (4, 3); (5, 2); (4, 4); (5, 3); (5, 4)). Từ đó \(n\left( E \right) = 6\) và \(P\left( E \right) = \frac{6}{{20}} = \frac{3}{{10}} = 0,3\)

Chú ý: Trong những phép thử đơn giản, ta đếm số phần tử của tập \(\Omega \) và số phần tử của biến cố E bằng cách liệt kê ra tất cả accs phần tử của hai tập hợp này. 

Qua thực tế người ta thấy rằng một biến cố có xác suất rất bé thì sẽ không xảy ra khi ta thực hiện một phép thử hay một vài phép thử. Từ đó người ta đã thừa nhận nguyên lí sau đây gọi là nguyên lí xác suất bé:

Nếu một biến có có xác suắt rất bé thì trong một phép thử biến cố đó sẽ không xảy ra.

Chẳng hạn, xác suất một chiếc máy bay rơi là rất bẻ, khoảng 0,00000027. Mỗi hành khách khi đi máy bay đều tin rằng biến cố: “Máy bay rơi” sẽ không xảy ra trong chuyến bay của mình, do đó người ta vẫn không ngân ngại đi máy bay.

Chú ý: Trong thực tế, xác suất của một biến cố được coi là bé phụ thuộc vào từng trường hợp cụ thể. Chẳng hạn, xác suất một chiếc điện thoại bị lối kĩ thuật là 0,001 được coi là rất bé, nhưng nếu xác suất cháy nỗ động cơ của một máy bay là 0,001 thỉ xác suất này không được coi là rất bé.