Cho hai điểm cố định và phân biệt \({F_1},{F_2}\). Đặt \({F_1}{F_2} = 2c > 0\). Cho số thực a lớn hơn c. Tập hợp các điểm M sao cho \(M{F_1} + M{F_2} = 2a\) được gợi là đường elip (hay elip). Hai điểm \({F_1},{F_2}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gợi là tiêu cự của elip đó.

Ví dụ: Cho lục giác đều ABCDEF. Chứng minh rằng bồn điểm B, C, E, F cùng thuộc một elip có hai tiêu điểm là A và D.

Giải

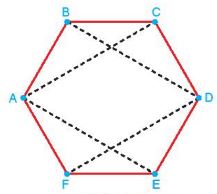
Lục giác đều ABCDEF có các cạnh bằng nhau và các góc đều có số đo là 120⁰ . Do đó, các tam giác ABC, BCD, DEF, EFA bằng nhau (c.g.c). Suy ra AC= BD= DF= AE.

Từ đó, ta có BA + BD= CA + CD= EA + ED= FA + FD > AD.

Vậy B, C. E, F cùng thuộc một elip có hai tiêu điểm là A và D.

Trong mặt phẳng toạ độ Oxy, elip có hai tiêu điểm thuộc trục hoành sao cho O là trung điềm của đoạn nối hai tiêu điểm đó, thì có phương trình \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a > b > 0\).             (2) Ngược lại, mỗi phương trình có dạng (2), với a > b > 0, đều là phương trình của elip có hai tiêu điểm \({F_1}\left( { – \sqrt {{a^2} – {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} – {b^2}} ;0} \right)\), tiêu cự \(2c = 2\sqrt {{a^2} – {b^2}} \) và tổng các khoảng cách từ mỗi điểm thuộc elip đó tới hai tiêu điểm bằng 2a. Phương trinh (2) được gọi là phương trình chính tắc của elip tương ứng.

Vi dụ: Cho elip có phương trình chính tắc \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của elip. Tính tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm.

Giải

Ta có: a² = 25, b² = 16. Do đó \(c = \sqrt {{a^2} – {b^2}}  = 3\). Vậy elip có hai tiêu điểm là \({F_1}\left( { – 3;0} \right);{F_2}\left( {3;0} \right)\) và tiêu cự là \({F_1}{F_2} = 2c = 6\). Ta có \(a = \sqrt {25}  = 5\), nên tổng các khoảng cách từ mỗi điểm trên elip tới hai tiêu điểm bằng 2a= 10.

Cho hai điểm phân biệt có định \({F_1}\) và \({F_2}\). Đặt \({F_1}{F_2} = 2c\). Cho số thực dương a nhỏ hơn c. Tập hợp các điểm M sao cho \(\left| {M{F_1} – M{F_2}} \right| = 2c\) được gọi là đường hypebol (hay hypebol). Hai điểm \({{F_1},{F_2}}\) được gọi là hai tiêu điểm và \({F_1}{F_2} = 2c\) được gọi là tiêu cự của hypebol đó.

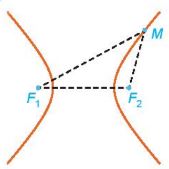
Chú ý: Hypebol có hai nhánh (Hình cho dưới), một nhánh gồm những điểm M thoả mãn MEF,~ ME, =2a và nhánh còn lại gồm những điểm M thoả mãn \(M{F_1} – M{F_2} =  – 2a\) (hay \(M{F_2} – M{F_1} = 2a\))

Ví dụ: Trên biển có hai đảo hình tròn với bán kính khác nhau. Tại vùng biển giữa hai đảo đó, người ta xác định một đường ranh giới cách đều hai đảo, tức là, đường mà khoảng cách từ mỗi vị trí trên đó đến hai đảo là bằng nhau. Hỏi đường ranh giới đó có thuộc một nhánh của một hypebol hay không?

Chú ý: Khoảng cách từ một vị trí trên biển đến đảo hinh tròn bằng hiệu của khoảng cách từ vị trí đó đến tâm đảo và bán kính của đảo.

Giải

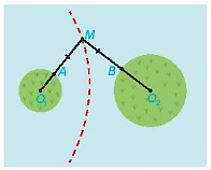
Giả sử đảo thứ nhất có tâm \({O_1}\) và bán kính \({R_1}\), đảo thứ hai có tâm \({O_2}\) và bán kinh \({R_2}\). Do hai đường
tròn \(\left( {{O_1};{R_1}} \right),\left( {{O_2};{R_2}} \right)\) nằm ngoài nhau nên \({O_1}{O_2} > {R_1} + {R_2}\). 

Gọi M là một điểm bất kì thuộc đường ranh giới.

Vì M cách đều hai đảo nên

\(M{O_1} – {R_1} = M{O_2} – {R_2} \Leftrightarrow M{O_1} – M{O_2} = {R_1} – {R_2}.\)

Vậy đường ranh giới thuộc một nhánh của hypebol với tiêu điểm \({F_1}\) trùng \({O_1}\), \({F_2}\) trùng \({O_2}\), \(2c = {O_1}{O_2},2{\rm{a}} = \left| {{R_1} – {R_2}} \right|.\) 

Trong mặt phẳng toạ độ Oxy, hypebol có hai tiêu điểm thuộc trục hoành sao cho O là trung điểm của đoạn nối hai tiêu điểm đó, thì có phương trình \(\frac{{{x^2}}}{{{a^2}}} – \frac{{{y^2}}}{{{b^2}}} = 1\) với \(a,b > 0\).      (4) Ngược lại, mỗi phương trình có dạng (4), với a, b >0, đều là phương trình của hypebol có hai tiêu điểm \({F_1}\left( { – \sqrt {{a^2} + {b^2}} ;0} \right),{F_2}\left( {\sqrt {{a^2} + {b^2}} ;0} \right)\), tiêu cự \(2c = 2\sqrt {{a^2} + {b^2}} \) và giá trị tuyệt đối của hiệu các khoảng cách từ mối điểm thuộc hypebol đến hai tiêu điểm bằng 2a. Phương trình (4) được gọi là phương trình chính tắc của hypebol tương ứng.

Ví dụ: Cho hypebol có phương trình chính tắc \(\frac{{{x^2}}}{9} – \frac{{{y^2}}}{{16}} = 1\). Tìm các tiêu điểm và tiêu cự của hypebol. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng bao nhiêu?

Giải

Ta có \({a^2} = 9,{b^2} = 16\), nên \(c = \sqrt {{a^2} + {b^2}}  = 5\). Vậy hypebol có hai tiêu điểm là \({F_1}\left( { – 5;0} \right),{F_2}\left( {5;0} \right)\) và có tiêu cự 2c = 10. Hiệu các khoảng cách từ một điểm nằm trên hypebol tới hai tiêu điểm có giá trị tuyệt đối bằng \(2{\rm{a}} = 2\sqrt 9  = 6\).

Cho một điểm F có định và một đường thẳng \(\Delta \) cố định không đi qua F. Tập hợp các điểm M cách đều F và \(\Delta \) được gọi là đường parabol (hay parabol). Điểm F được gọi là tiêu điểm, \(\Delta \) được gọi là đường chuẩn, khoảng cách từ F đến \(\Delta \) được gọi là tham số tiêu của parabol đó.  Xét (P) là một parabol với tiêu điểm F, đường chuẩn \(\Delta \). Gọi H là hình chiếu vuông góc của F trên \(\Delta \). Khi đó, trong hệ trục toạ độ Oxy với gốc O là trung điểm của HF, tia Ox trùng tia OF, parabol (P) có phương trình \({y^2} = 2p{\rm{x}}\) (với p > 0)        (5) Phương trình (5) được gọi là phương trình chính tắc của parabol (P). Ngược lại, mỗi phương trình dạng (5), với p > 0, là phương trình chính tắc của parabol có tiêu điểm \(F\left( {\frac{p}{2};0} \right)\) và đường chuẩn \(\Delta 😡 =  – \frac{p}{2}\).

Ví dụ: Cho parabol \((P):{y^2} = x\). 

a) Tìm tiêu điểm F, đường chuẩn \(\Delta \) của (P).

b) Tìm những điểm trên (P) có khoảng cách tới F bằng 3. 

Giải

a) Ta có 2p = 1 nên \(p = \frac{1}{2}\). 

Parabol có tiêu điểm \(F\left( {\frac{1}{4};0} \right)\) và đường chuẩn \(\Delta 😡 =  – \frac{1}{4}\) 

b) Điểm \(M\left( {{x_0};{y_0}} \right)\) thuuọc (P) có khoảng các tới F bằng 3 khi và chỉ khi \({y_0}^2 = {x_0}\) và MF = 3.

Do \(MF = d\left( {M,\Delta } \right)\) nên \(d\left( {M,\Delta } \right) = 3\)

Mặt khác \(\Delta 😡 + \frac{1}{4} = 0\) và \({x_0} = {y_0}^2 \ge 0\) nên \(3 = d\left( {M,\Delta } \right) = \left| {{x_0} + \frac{1}{4}} \right| = {x_0} + \frac{1}{4}.\)

Vậy \({x_0} = \frac{{11}}{4}\) và \({y_0} = \frac{{\sqrt {11} }}{2}\) hoặc \({y_0} =  – \frac{{\sqrt {11} }}{2}\). 

Vậy có hai điểm M thoả mãn bài toán với toạ độ là \(\left( {\frac{{11}}{4};\frac{{\sqrt {11} }}{2}} \right)\) và \(\left( {\frac{{11}}{4}; – \frac{{\sqrt {11} }}{2}} \right)\). 

a) Tính chất quang học

Tương tự gương cầu lồi thường đặt ở những khúc đường cua, người ta cũng có những gương (lồi, lõm) elip, hypebol, parabol. Tia sáng gặp các gương này, đều được phản xạ theo một quy tắc được xác định rõ bằng hình học, chẳng hạn:

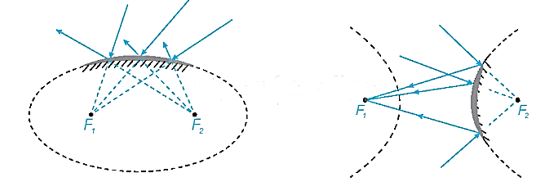
+ Tia sáng phát ra từ một tiêu điểm của elip, hypebol (đối với các gương lõm elip, hypebol) sau khi gặp elip, hypebol sẽ bị hắt lại theo một tia (tia phản xạ) nằm trên đường thẳng đi qua tiêu điểm còn lại.

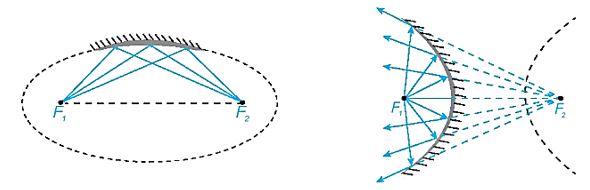
+ Tia sáng hướng tới một tiêu điểm của elip, hypebol (đối với các gương elip, hypebol lồi), khi gặp elip, hypebol sẽ bị hắt lại theo một tia nằm trên đường thẳng đi qua tiêu điểm còn lại. 

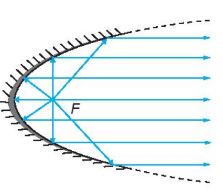
+ Với gương parabol lõm, tia sáng phát ra từ tiêu điểm khi gặp parabol sẽ bị hát lại theo một tia vuông góc với đường chuẩn của parabol. Ngược lại, nều tia tới vuông góc với đường chuẩn của parabol thì tia phản xạ sẽ đi qua tiêu điểm của parabol

Tính chất quang học được đề cập ở trên giúp ta nhận được ánh sáng mạnh hơn khi các tỉa sáng hội tụ và giúp †a đổi hướng ánh sáng khi cần. Ta cũng có điều tương tự đối với tin hiệu âm thanh, tín hiệu truyền từ vệ tinh.

b) Một số ứng dụng

Ba đường conic xuât hiện và có nhiêu ứng dụng trong khoa học và trong cuộc sông, chẳng hạn:

+ Tia nước bắn ra từ đài phun nước, đường đi bỗng của quả bóng là những hình ảnh về đường parabol;

+ Khi nghiêng cốc tròn, mặt nước trong cốc có hình elip. Tương tự, dưới ánh sáng mặt trời, bóng của một quả bóng, nhìn chung, là một elip;

+ Ánh sáng phát ra từ một bóng đèn Led trên trằn nhà có thể tạo nên trên tường các nhánh hypebol;

+ Nhiều công trình kiến trúc có hình elip, parabol hay hypebol.

……