Nếu với mỗi giá tị của x thuộc tập hợp số D có một và chỉ một giá trị tương ứng của y thuộc tập số thực R thì ta có một hàm số. Ta gọi x là biến số và y là hàm số của x. Tập hợp D gọi là tập xác định của hàm số. Tập tắt cả các giá trị y nhận được, gọi là tập giá trị của hàm số.

Ví dụ: Viết hàm số mô tả sự phụ thuộc của quãng đường đi được vảo thời gian của một vật chuyển động thẳng đều với vận tốc 2 m/s. Tìm tập xác định của hàm số đó. Tính quãng đường vật đi được sau 5s, 10s.

Giải

Một vật chuyển động thẳng đều với vận tốc v = 2 m/s thì quãng đường đi được S (mét) phụ thuộc vào thời gian t (giây) theo công thức S = 2t, trong đó t lả biến số, S = S(t) là hàm số của t.

Tập xác định của hàm số là Ð= [0; +).

Quảng đường vật đi được sau 5s là: S₁ = S(5) = 2.5 = 10 (m).

Quảng đường vật đi được sau 10s là: S₂ = S(10) = 2.10 = 20 (m).

Chú ý: Khi cho hàm số bằng công thức y= f(x) mà không chỉ rõ tập xác định của nó thì ta quy ước tập xác định của hàm số là tập hợp tất cả các số thực x sao cho biểu thức f(x) có nghĩa.

Đồ thị hàm số y = f(x) xác định trên tập D là tập hợp tất cả các điểm M(x; f(x)) trên mặt phẳng toạ độ với mọi x thuộc D.

Ví dụ: Viết công thức của hàm số cho ở HĐ3b. Tìm tập xác định, tập giá trị và vẽ đồ thị của hàm số này.

Giải

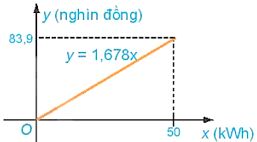
Công thức của hàm số cho ở HĐ3b là y = 1,678x với \(0 \le x \le 50\).

Tập xác định của hàm số này là D = [0: 50]

Vi \(0 \le x \le 50\) nên \(0 \le y \le 1,678.50 = 83,9\). 

Vậy tập giá trị của hàm số là [0; 83,9].

Đỏ thị của hàm số y = 1,678x trên [0; 50] là một đoạn thẳng.

Hàm số y = f(x) được gọi là đồng biến (tăng) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\).  Hàm số y = f(x) được gọi là nghịch biến (giảm) trên khoảng (a; b), nếu \(\forall {x_1},{x_2} \in \left( {a,b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\).

Ví dụ: Hàm số y = x² đồng biến hay nghịch biến trên mỗi khoảng \(\left( { – \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\)?

Giải

Vẽ đồ thị hàm số y= f{x) = x² như hình sau:

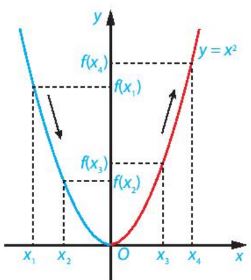
+ Trên khoảng \(\left( { – \infty ;0} \right)\), đồ thị “đi xuống” từ trái sang phải và với \({x_1},{x_2} \in \left( { – \infty ;0} \right)\), \({x_1} < {x_2}\) thì \(f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\). Như vậy hàm số y = x² nghịch biến trên khoảng \(\left( { – \infty ;0} \right)\). 

+ Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị “đi lên” từ trái sang phải và với \({x_3},{x_4} \in \left( {0; + \infty } \right)\), \({x_3} < {x_4}\) thì \(f\left( {{x_3}} \right) < f\left( {{x_4}} \right)\). Như vậy, hàm số y = x² đồng biến trên khoảng \(\left( {0; + \infty } \right)\). 

Chú ý

+ Đỗ thị của một hàm số đồng biến trên khoảng (a; b) là đường “đi lên” từ trái sang phải;

+ Đồ thị của một hàm số nghịch biến trên khoảng (a; b) là đường “đi xuống” từ trái sang phải.