a) Quy tắc cộng

Giả sử một công việc có thể được thực hiện theo phương án A hoặc phương án B. Phương án A có m cách thực hiện, phương án B có n cách thực hiện không trùng với bất kì cách nào của phương án A. Khi đó, công việc có thể thực hiện theo m + n cách.

b) Quy tắc nhân

Giả sử một công việc được chúa thành hai công đoạn. Công đoạn thứ nhât có m cách thực hiện và ứng với mỗi cách đó có n cách thực hiện công đoạn thứ hai. Khi đó, công việc có thể thực hiện theo m.n cách.

a) Hoán vị

Cho tập hợp A có n phần tử (\(n \ge 1\)). Mỗi cách sắp xếp n phản tử của A theo một thứ tự gợi là một hoán vị các phần tử đó (gọi tắt là hoán vị của A hay của n phân tử).

Kí hiệu Pn là số hoán vị của n phần tử

Người ta chứng minh được rằng:

Số các hoán vị của m phần tử (\(n \ge 1\)) bằng

\({P_n} = n\left( {n – 1} \right)\left( {n – 2} \right)…2.1.\)

Chú ý:

+ Ta đưa vào kí hiệu: \(n! = n\left( {n – 1} \right)\left( {n – 2} \right)…2.1.\) và đọc là n giai thừa hoặc giai thừa của n.

Khi đó, Pn = n!.

+ Quy ước: 0! =1.

b) Chỉnh hợp

Cho tập hợp A có n phân tử (\(n \ge 1\)) và sô nguyên k với \(1 \le k \le n\).  Mỗi cách lây k phần tử của A và sắp xếp chúng theo một thứ tự gọi là một cchỉnh hợp chập k của n phần tử đó. Kí hiệu \(A_n^k\) là số chỉnh hợp chập k của n phần tử.

Người ta chứng minh được rằng

Số các chỉnh hợp chập k của n phân tử \(1 \le k \le n\) bằng

\(A_n^k = n\left( {n – 1} \right)\left( {n – 2} \right)…\left( {n – k + 1} \right) = \frac{{n!}}{{\left( {n – k} \right)!}}\). 

Nhận xét: Mỗi hoán vị của n phần tử cũng chính là chỉnh hợp chập n của n phần tử đó.

Ta có: \({P_n} = A_n^k,n \ge 1.\) 

c) Tổ hợp

Cho tập hợp A có n phân tử (\(n \ge 1\))  Mỗi tập con gồm k phần tử (\(1 \le k \le n\)) của A được gọi là một tổ hợp chập k của n phân tử.

Kí hiệu \(C_n^k\) là số tổ hợp chập k của n phần tử \(1 \le k \le n\)

Người ta chứng minh được rằng:

Số các tổ hợp chập k của n phần tử \(1 \le k \le n\) bằng

\(C_n^k = \frac{{n!}}{{k!\left( {n – k} \right)!}}\)

Chú ý: Người ta quy ước \(C_n^0 = 1\). 

Ta có hai công thức khai triển sau:

\(\begin{array}{l} \begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^4} = {C_4}^0{a^4} + {C_4}^1{a^3}b + {C_4}^2{a^2}{b^2} + {C_4}^3a{b^3} + {C_4}^4{b^4}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^4} + 4{a^3}b + 6{a^2}{b^2} + 4a{b^3} + {b^4}.} \end{array}\\ \begin{array}{*{20}{l}} {{{\left( {a + b} \right)}^5} = {C_4}^0{a^5} + {C_5}^1{a^4}b + {C_5}^2{a^3}{b^2} + {C_5}^3{a^2}{b^3} + {C_5}^4a{b^4} + {C_5}^5{b^5}}\\ {\;\;\;\;\;\;\;\;\;\;\;\;\; = {a^5} + 5{a^4}b + 10{a^3}{b^2} + 10{a^2}{b^3} + 5a{b^4} + {b^5}.} \end{array} \end{array}\) Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) \({\left( {a + b} \right)^n}\) ứng với n = 4 và n = 5.

Chú ý:

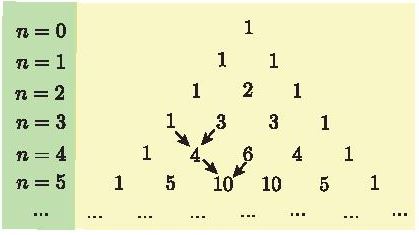
Các hệ số trong khai triển nhị thức Newton \({\left( {a + b} \right)^n}\) với n =0; 1; 2; 3;..  được viết thành từng hàng và xếp thành bảng số như bên. Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của hai số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).

Bảng số trên được gọi là tam giác Pasca (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 — 1662).