1.1. Nhắc lại về tập hợp
Ở cấp Trung học cơ sở, trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.
Ví dụ:
a) Các học sinh của lớp 10A tạo thành một tập hợp. Các học sinh nữ của lớp này cũng tạo thành một tập hợp.
b) Các nghiệm của phương trình x2 — 4= 0 tạo thành một tập hợp (gọi là tập nghiệm của phương trình x2 — 4= 0). Tập hợp này có hai phân tử là 2 và – 2.
Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa A, B, C….. và kí hiệu phần tử của tập hợp bằng các chữ cái in thường a, b, c,…
Chú ý: Đôi khi, để ngắn gọn người ta dùng từ “tập” thay cho “tập hợp”.
Để chỉ a là một phần tử của tập hợp A, ta viết a \(\in\) A (đọc là “a thuộc A”). Đề chỉ a không là phần tử của tập hợp A, ta việt a \(\notin\) A (đọc là *a không thuộc A”).
*Cách xác định tập hợp
Xét tập hợp A các số tự nhiên chẫn nhỏ hơn 15. Ta có thể viết tập hợp A đưới dạng điệt kê các phẩn tử.
A = {0;2; 4; 6: 8; 10; 12; 14},
hoặc dưới dang chỉ ra tỉnh chất đặc trưng cho các phân tử:
A = {x | x \(\in\) N, x chẵn và x < 15}
Chú ý: Khi liệt kê các phần tử của tập hợp, ta có một số chủ ý sau đây:
a) Các phần tử có thể được viết theo thứ tự tùy ý. Chẳng hạn, đễ viết tập hợp A các nghiêm của phương trình x(x – 1) =0, ta có thể viết A = {0; 1} hoặc A= {1:0}.
b) Mỗi phân tử chỉ được liệt kề một lần. Chẳng hạn, nêu kí hiệu B là tập hợp các chữ cái tiếng Anh trong tử *mathematics” thì B = (m; a; t; h; e; i; c; s}
c) Nếu quy tắc xác định các phân tử đủ rõ thì người ta dùng “…” mà không nhất thiết viết ra tắt cả các phần tử của tập hợp. Chẳng hạn, tập hợp các số tự nhiên không quá 100 có thể được viết là {0; 1; 2; …; 100}.
Ví dụ: Viết mỗi tập hợp sau đưới đạng thích hợp:
a) Tập hợp A các ước đường của 18;
b) Tập hợp B các nghiệm của phương trình x2 + 3x – 4 = 0;
c) Tập hợp C các số tự nhuên lẻ;
4) Tập hợp D các nghiệm của phương trình x + 3y = 1.
Giải
a) Số 18 cỏ các ước đương là 1; 2; 3; 6; 9; 18. Do đó A = (1; 2; 3; 6; 9; 18}
b) Giải phương trình x2 + 3x – 4 = 0 nhận được hai nghiệm 1 và – 4. Do đỏ B = {1, – 4}. Ta cũng có thể viết \(B = {\rm{\{ }}x \in R|{x^{2\;}} + 3x – 4 = 0{\rm{\} }}\)
c) Ta có thể viết đưởi dang liệt kê các phần tử: C= (1; 3; 5; 7;…}. Ta cũng có thể viết dười dạng chỉ ra tính chất đặc trưng cho các phần tử: C = {x | x \(\in\) N, x là số lẻ} hoặc C= (x \(\in\) N |x là số lẻ) hoặc C= {x | x=2n+ 1, x \(\in\) N).
d) Ta viết D = {(x, y) | x,y \(\in\) R, x + 3y = 1}.
Chú ý: Có những tập hợp, như A và B ở Ví dụ trên, ta có thể đếm hết các phân tử của chúng. Những tập hợp như vậy được g
Nếu E là tập hợp hữu hạn thì số phần tử của nó được kí hiệu là n(E). Chẳng hạn. trong Vi dụ trên, ta có: n(A) = 6 và n(B) = 2.
Đặc biệt, n(Ø) = 0.
1.2. Tập con và hai tập hợp bằng nhau
|
Cho hai tập hợp A và B. Nếu mọi phân tử của A đều là phân từ của B thì ta nói tập hợp A là rập con của tập hợp B và kí hiệu \(A \subset B\) (đọc là A chứa trong B), hoặc \(B \supset A\) (đọc là B chứa A) |
|---|
Nhận xét
* \(A \subset A\) và \(Ø \subset A\) với mọi tập hợp A.
* Nếu A không phải là tập con của B thì ta kí hiệu \(A \not\subset B\) (đọc là A không chứa trong B hoặc B không chứa A).
* Nếu \(A \subset B\) hoặc \(B \subset A\) thì ta nói A và B có quan hề bao hàm.
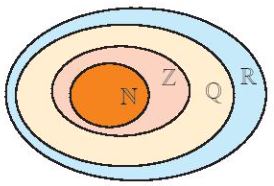
Chú ý: Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu tỉ, tập số thực), ta có quan hệ bao hàm: \(N \subset Z \subset Q \subset R\)
Ví dụ: Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.
a) \(A = \{ – 1;1\} \) và \(B = \{ – 1;0;1;2\} \)
b) \(A = \mathbb{N}\) và \(B = \mathbb{Z}\)
c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.
d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.
Giải
a) Có vì \( – 1 \in B,\;1 \in B\).
b) Có vì các số tự nhiên cũng là số nguyên.
c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.
d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.
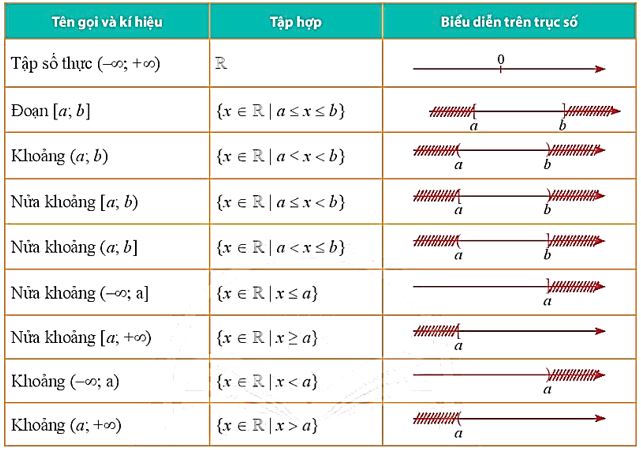
1.3. Một số tập con của tập hợp số thực
Sau này ta thường sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a < b)