|
Bất phương trình bậc lai một ẩn x là bất phương trình có một trong các dạng \(a{x^2} + b{\rm{x}} + c \le 0,a{x^2} + b{\rm{x}} + c < 0,a{x^2} + b{\rm{x}} + c \ge 0,a{x^2} + b{\rm{x}} + c > 0\) với \(a \ne 0\). Nghiệm của bất phương trình bậc hai là các giá trị của biến x mà khi thay vào bất phương trình ta được bắt đẳng thúc đúng. |
|---|
Ví dụ: Các bất phương trình nào sau đây là bắt phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn. x = 1 và x= 2 có lả nghiệm của bắt phương trình đó hay không?
\(\begin{array}{l}
a){x^2} + x – 3 \ge 0;\\
b)3{x^3} + {x^2} – 1 \le 0.
\end{array}\)
Giải
3) \({x^2} + x – 3 \ge 0\) là một bât phương trình bậc hai một ân.
Vì \({1^2} + 1 – 3 = – 1 < 0\) nên x = 1 không là nghiệm của bất phương trình trên.
Vì \({2^2} + 2 – 3 = 3 > 0\) nên x = 2 là một nghiệm của bất phương trình trên.
b) \(3{x^3} + {x^2} – 1 \le 0\) không phải là một bât phương trình bậc hai một ẩn.
| Giải bất phương trình bậc hai là tìm tập hợp các nghiệm của bât phương trình đó. |
|---|
Ta có thể giải bắt phương trình bậc hai bằng cách xét dâu của tam thức bậc hai tương ứng.
Ví dụ: Giải bất phương trình bậc hai \(6{x^2} + 7x – 5 > 0\)
Giải
Tam thức bậc hai \(f(x) = 6{x^2} + 7x – 5\) có hai nghiệm phân biệt là \({x_1} = – \frac{5}{3}\) và \({x_2} = \frac{1}{2}\).
a = 6 > 0 nên f(x) đương với mọi x thuộc hai khoảng \(\left( { – \infty ; – \frac{5}{3}} \right),\left( {\frac{1}{2}; + \infty } \right)\)
Vậy bất phương trình \(6{x^2} + 7x – 5 > 0\) có tập nghiệm là \(\left( { – \infty ; – \frac{5}{3}} \right) \cup \left( {\frac{1}{2}; + \infty } \right)\)
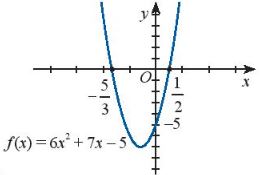
Lưu ý: Có thể sử dụng đồ thị hàm số \(f(x) = 6{x^2} + 7x – 5\) (Hình trên) để giải bất phương trình ƒ(x) > 0.