*Phương trình tham số của đường thẳng

Cho đường thẳng \(\Delta \) đi qua điểm \(A\left( {{x_0};{y_0}} \right)\) và có vectơ chỉ phương \(\overrightarrow u \left( {a;b} \right)\). Khi đó điểm M(x: y) thuộc đường thẳng \(\Delta \) khi và chỉ khi tổn tại số thực t sao cho \(\overrightarrow {AM}  = t\overrightarrow u \), hay \(\left\{ \begin{array}{l} x = {x_0} + at\\ y = {y_0} + bt \end{array} \right.\;\;\;\;\;\;\;\;(2)\) Hệ (2) được gọi là phương trình tham số của đường thẳng \(\Delta \) (t là tham số).

Ví dụ: Lập phương trình tham số của đường thẳng \(\Delta \) đi qua điểm A(2; -3) và có vectơ chỉ phương \(\overrightarrow u \left( {4; – 1} \right)\).

Giải

Phương trinh tham số của đường thẳng \(\Delta \) là \(\left\{ \begin{array}{l}
x = 2 + 4t\\
y =  – 3 – t
\end{array} \right.\)

*Phương trình tổng quát của đường thẳng

Trong mặt phẳng toạ độ, mọi đường thẳng đều có phương trình tổng quát dạng ax + by + c =0, với a và b không đồng thời bằng 0. Ngược lại, mỗi phương trình dạng ax + by + c =0, với a và b không đồng thời bằng 0, đều là phương trình của một đường thẳng, nhận \(\overrightarrow n \left( {a;b} \right)\) là một vectơ pháp tuyến.

Ví dụ: Trong mặt phẳng toạ độ, lập phương trình tổng quát của đường thẳng \(\Delta \) đi qua điểm A(2: 1) và nhận \(\overrightarrow n \left( {3;4} \right)\) là một vectơ pháp tuyến.

Giải

Đường thẳng \(\Delta \) có phương trình là 3(x – 2)+ 4(y – 1) = 0 hay 3x + 4y – 10 = 0

Nhận xét: Trong mặt phẳng toạ độ, cho đường thẳng \(\Delta \): ax + by + c = 0

+ Nếu b = 0 thì phương trình \(\Delta \) có thể đưa về dạng x = m (với \(m =  – \frac{c}{a}\)) và \(\Delta \) vuông góc với Ox.

+ Nếu \(b \ne 0\) thì phương trình \(\Delta \) có thể đưa về dạng y =  nx + p (với \(n =  – \frac{a}{b},p =  – \frac{c}{b}\))

* Liên hệ giữa đồ thị hàm số bậc nhất và đường thẳng 

+ Nếu a=0 và b \( \ne \) 0 thì phương trình tổng quát ax + by + c =0 trở thành y

Khi đó d là đường thẳng vuông góc với Oy tại điểm \(y =  – \frac{c}{b}\) (Hình sau).

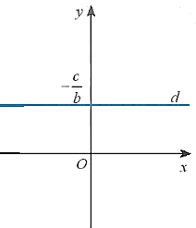
+ Nếu b =0 và a \( \ne \) 0 thì phương trình tổng quát ax + by + c =0 trở thành \(x =  – \frac{c}{a}\)

Khí đó d là đường thẳng vuông góc với Ox tại điểm \(\left( { – \frac{c}{a};0} \right)\) (Hình sau)

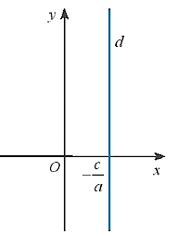
Trong cả hai trường hợp này, đường thẳng d không phâi là đồ thị của hàm số bậc nhất.

Cho \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\).

Toạ độ giao điểm của \({\Delta _1}\) và \({\Delta _2}\) là nghiệm của hệ phương trình: 

\(\left\{ \begin{array}{l}
{a_1}x + {b_1}y + {c_1} = 0\\
{a_2}x + {b_2}y + {c_2} = 0
\end{array} \right.(*)\)

\({\Delta _1}\) cắt \({\Delta _2}\) tại \(M\left( {{x_0};{y_0}} \right)\) ⇔ hệ (*) có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\). \({\Delta _1}\) song song với \({\Delta _2}\) ⇔ hệ (*) vô nghiệm. \({\Delta _1}\) trùng \({\Delta _2}\) ⇔ hệ (*) có vô số nghiệm.

Chú ý

Dựa vào các vectơ chỉ phương \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) hoặc các vectơ pháp tuyến \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) của \(\overrightarrow {{\Delta _1}} ,\overrightarrow {{\Delta _2}} \) ta có: 

+ \({{\Delta _1}}\) Và \({{\Delta _2}}\) song song hoặc trùng nhau ⇔ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) cùng phương ⇔ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) cùng phương. 

+ \({{\Delta _1}}\) và \({{\Delta _2}}\) cắt nhau ⇔ \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \) không cùng phương ⇔ \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \) không cùng phương. 

Ví dụ: Xét vị trí tương đối giữa đường thẳng \(\Delta 😡 – \sqrt 2 y + 4\sqrt 3  = 0\) và mỗi đường thẳng sau:

\(\begin{array}{l}
{\Delta _1}:\sqrt 3 x – \sqrt 6 y + 12 = 0;\\
{\Delta _2}:\sqrt 2 x – 2y = 0.
\end{array}\)

Giải

Vì \(\begin{array}{l}
x – \sqrt 2 y + 4\sqrt 3  = 0 \Leftrightarrow \sqrt 3 \left( {x – \sqrt 2 y + 4\sqrt 3 } \right) = 0\\
\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \Leftrightarrow \sqrt 3 x – \sqrt 6 y + 12 = 0.
\end{array}\)

Vậy \({{\Delta}}\) và \({{\Delta _1}}\) là một, tức là chúng trùng nhau. 

Hai đường thẳng \({{\Delta}}\) và \({{\Delta _2}}\) có hai vectơ pháp tuyến \(\overrightarrow n \left( {1; – \sqrt 2 } \right)\) và \(\overrightarrow {{n_2}} \left( {\sqrt 2 ; – 2} \right)\) cùng phương. 

Do đó, chúng song song hoặc trùng nhau. Mặt khác, điểm O(0; 0) thuộc đường thẳng \({{\Delta _2}}\) nhưng không thuộc đường thẳng \({{\Delta}}\) nên hai đường thẳng này không trùng nhau.

Vậy \({{\Delta}}\) và \({{\Delta _2}}\) song song với nhau.

– Hai đường thẳng cắt nhau tạo thành bốn góc, số đo của góc không tù được gọi là số đo góc (hay đơn giản là góc) giữa hai đường thẳng. – Góc giữa hai đường thẳng song song hoặc trùng nhau được quy ước bằng 0°. – Cho hai đường thẳng \({\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0\) và \({\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0\). Với các vectơ pháp tuyến \(\overrightarrow {{n_1}} \left( {{a_1};{b_1}} \right)\) và \(\overrightarrow {{n_2}} \left( {{a_2};{b_2}} \right)\) trong ứng. Khi đó, góc \(\varphi \) giữa hai đường thằng đó được xác định thông qua công thức \(cos\varphi  = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {{a_1}^2 + {b_1}^2} .\sqrt {{a_2}^2 + {b_2}^2} }}\)

Ví dụ: Tỉnh góc giữa hai đường thằng

\({\Delta _1}:\sqrt 3 x – y + 2 = 0\) và \({\Delta _2}:x – \sqrt 3 y – 2 = 0\). 

Giải

Vectơ pháp tuyến của \({{\Delta _1}}\) là \(\overrightarrow {{n_1}}  = \left( {\sqrt 3 ; – 1} \right)\), của \({{\Delta _2}}\) là \(\overrightarrow {{n_2}}  = \left( {1; – \sqrt 3 } \right)\).

Gọi \(\varphi \) là góc giữa hai đường thẳng \({{\Delta _1}}\) và \({{\Delta _2}}\). Ta có

\(cos\varphi  = \left| {cos\left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \frac{{\left| {\sqrt 3 .1 + \left( { – 1} \right).\left( { – \sqrt 3 } \right)} \right|}}{{\sqrt {{{\left( {\sqrt 3 } \right)}^2} + {{\left( { – 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { – \sqrt 3 } \right)}^2}} }} = \frac{{\sqrt 3 }}{2}.\)  

Do đó, góc giữa \({{\Delta _1}}\) và \({{\Delta _2}}\) là \(\varphi  = {30^0}\). 

Cho điểm \(M\left( {{x_0};{y_0}} \right)\) và đường thẳng \(\Delta :ax + by + c = 0\). Khoảng cách từ điểm M đến đường thẳng \(\Delta \), kí hiệu là \(d\left( {M,\Delta } \right)\), được tính bởi công thức \(d\left( {M,\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}\)

Ví dụ: Tính khoảng cách từ điểm M(2; 4) đến đường thẳng \(\Delta :3x + 4y – 12 = 0.\) 

Giải

Áp dụng công thức tính khoảng cách từ điểm M đến đường thẳng \(\Delta\), ta có

\(d\left( {M,\Delta } \right) = \frac{{\left| {3.2 + 4.4 – 12} \right|}}{{\sqrt {{3^2} + {4^2}} }} = \frac{{10}}{5} = 2\)

Vậy khoảng cách từ điểm M đến đường thẳng \(\Delta\) là 2.