+) Định nghĩa: Giả sử x và y là hai đại lượng biến thiên, \(x \in D\) Nếu với mỗi \(x \in D\), ta xác định được y duy nhất (\(y \in \mathbb{R}\)) thì ta có một hàm số. +) Tên gọi: x là biến số, y là hàm số của x, D là tập xác định \(T = \left\{ {y|x \in D} \right\}\) là tập giá trị của hàm số. +) Ta thường kí hiệu \(f(x)\) là giá trị y tương ứng với x, nên hàm số thường viết là \(y = f(x)\)

Chú ý

+ Hàm số cho bởi công thức mà không chỉ rõ tập xác định thì

TXĐ của hàm số \(y = f(x)\) là tập hợp tất cả các \(x \in \mathbb{R}\) sao cho \(f(x)\) có nghĩa.

+ Một hàm số có thể được cho bởi hay nhiều công thức.

Ví dụ: Tìm tập xác định của các hàm sô sau:

\(\begin{array}{l}
a)f\left( x \right) = \sqrt {5 – x} \\
b)f\left( x \right) = \frac{1}{{2x – 6}}
\end{array}\)

Giải

a) Biểu thức f(x) có nghĩa khi và chỉ khi \(5 – x \ge 0\), tức là khi \(x \le 5\).

Vậy tập xác định của hàm số này là \(D = \left( { – \infty ;5} \right]\).

b) Biểu thức f(x) có nghĩa khi và chỉ khi \(2x – 6 \ne 0\), tức là khi \(x \ne 3\). 

Vậy tập xác định của hàm số này là \(D = R\backslash \left\{ 3 \right\}\). 

Cho hàm số y = f(x) có tập xác định D

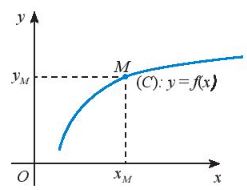
Trên mặt phẳng tọa độ Oxy, đồ thị (C) của hàm số là tập hợp tất cả các điểm M(x; y) với \({x \in D}\) và y = f(x).

Chú ý: Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\) khi và chỉ khi \({{x_M} \in D}\) và \({{y_M} = f({x_M})}\).

 

Với hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\), ta nói: – Hàm số đồng biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\) – Hàm số nghịch biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)

Nhận xét:

Khi hàm số đồng biến (tăng) trên khoảng (a; b) thì đồ thị của nó có dạng đi lên từ trái sang phải. Ngược lại, khi hàm số nghịoh biển (giảm) trên khoảng (a; b) thì đồ thị của nó có dạng đi xuống từ trái sang phải.

Ví dụ: Gia đình bạn Sơn sống ở tầng ba, bà ngoai của Sơn sống ở tầng sáu thuộc cùng một chung cư cao tầng. Sơn đi bộ từ nhà mình xuống tàng một đề lấy thư và đưa lên nhà bà ngoại. Đưa thư cho bà xong, Sơn quay về nhà mình.

Đặt y = h(t) là hàm số biểu thị khoảng cách từ vị trí của Sơn đến mặt đất theo thời gian t từ khi bạn ấy bắt đầu đi cho đền khi về lại nhà mình (chọn gốc thời gian là lúc Sơn bắt đầu đi lây thư).

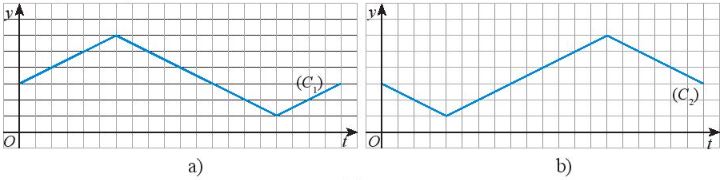
(C₁) hay (C₂) là đồ thị của hàm số y = h(t)? Tại sao?

Giải

Khi bắt đầu đi từ tầng ba xuống tầng một, Sơn ngày càng gần mặt đất nên khoảng cách từ vị trí của Sơn đên mặt đât giảm đân, hay hàm số giảm, vậy đô thị phải có
đạng đi xuống.

Khi đi từ tầng một lên tầng sáu đề đưa thư cho bà ngoại, Sơn ngày càng xa mặt đất nên khoảng cách từ vị trí của Sơn đến mặt đất tăng dần, hay hàm số tăng, vậy đồ thị phải có dạng đi lên

Khi đi từ tầng sáu về nhà mình, Sơn ngày càng gần mặt đất nên khoảng cách từ vị trí của Sơn đền mặt đất giảm dân, hay hàm số giảm, vậy đồ thi phải có đang đi xuống.

Đồ thi (C₂) có dạng tương ứng như mô tả ở trên. Do đó, (C₂) là đồ thị của hàm số y = h(t) này.