1.1. Định nghĩa
|
+) Tích của một số thực \(k\) với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí kiệu là \(k\overrightarrow a .\) +) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\) |
|---|
+) Quy ước: \(0\;\overrightarrow a = \overrightarrow 0 \) và \(k\;\overrightarrow 0 = \overrightarrow 0 \)
Ví dụ: Cho B là trung điểm của đoạn thảng AC. Tìm số k trong mỗi trường hợp sau:
a) \(\overrightarrow {CA} = k\overrightarrow {CB} \)
b) \(\overrightarrow {CA} = k\overrightarrow {AB} \)
Giải
Ta có: \(\overrightarrow {CA} ,\overrightarrow {CB} \) là hai vectơ cùng phương và \(\left| {\overrightarrow {CA} } \right| = 2\left| {\overrightarrow {CB} } \right|\)
Suy ra \(\overrightarrow {CA} = 2\overrightarrow {CB} \). Vậy k = 2
b) Ta có: \(\overrightarrow {CA} ,\overrightarrow {AB} \) là hai vectơ ngược hướng và \(\left| {\overrightarrow {CA} } \right| = 2\left| {\overrightarrow {AB} } \right|{\rm{ }}\)
Suy ra: \(\overrightarrow {CA} = – 2\overrightarrow {AB} \). Vậy k = -2
1.2. Tính chất
Với hai vecto \(\overrightarrow a ,\overrightarrow b \) và hai số thực \(k,t\) ta luôn có:
\(\begin{array}{l}k(t\overrightarrow a ) = (kt)\;\overrightarrow a \\(k + t)\,\overrightarrow a = k\overrightarrow a + t\overrightarrow a \\k(\overrightarrow a + \overrightarrow b ) = k\overrightarrow a + k\overrightarrow b ;\quad k(\overrightarrow a – \overrightarrow b ) = k\overrightarrow a – k\overrightarrow b \\1\;\overrightarrow a = \overrightarrow a ;\;\;( – 1)\;\overrightarrow a = – \,\overrightarrow a \end{array}\)
Ví dụ: Thực hiện các phép toán vecto sau:
\(\begin{array}{l}
a)5\left( {\overrightarrow u + \overrightarrow v } \right)\\
b)\left( {x + 2} \right)\overrightarrow a \\
c) – 3\left( {4\overrightarrow e } \right)\\
d)\overrightarrow c – 2\overrightarrow c
\end{array}\)
Giải
\(\begin{array}{l}
a)5\left( {\overrightarrow u + \overrightarrow v } \right) = 5\overrightarrow u + 5\overrightarrow v \\
b)\left( {x + 2} \right)\overrightarrow a = x\overrightarrow a + 2\overrightarrow a \\
c) – 3\left( {4\overrightarrow e } \right) = \left( { – 3.4} \right)\overrightarrow e = – 12\overrightarrow e \\
d)\overrightarrow c – 2\overrightarrow c = \left( {1 – 2} \right)\overrightarrow c = \left( { – 1} \right)\overrightarrow c = – \overrightarrow c
\end{array}\)
1.3. Một số ứng dụng
– Nếu I là trung điểm của đoạn thẳng AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \) với điểm M bất kì.
– Nếu G là trọng tâm của tam giác ABC thì \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 2\overrightarrow {MG} \) với điểm M bất kì.
* Điều kiện để hai vectơ cùng phương. Điều kiện để ba điểm thẳng hàng.
– Điều kiện cần và đủ để hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) (\(\overrightarrow b \ne \overrightarrow 0 \)) cùng phương là có một số thực k để \(\overrightarrow a = k\overrightarrow b \).
– Điều kiện cần và đủ để ba điểm phân biệt A, B, C thẳng hàng là có số thực k để \(\overrightarrow {AB} = k\overrightarrow {AC} \).
Ví dụ: Cho tam giác OAB. Điểm M thuộc cạnh AB sao cho \(AM = \frac{2}{3}AB\). Kẻ MH // OB, MK // OA (Hình sau).
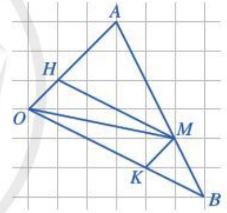
Giả sử \(\overrightarrow {OA} = \overrightarrow a ,\overrightarrow {OB} = \overrightarrow b \).
a) Biểu thị \(\overrightarrow {OH}\) theo \(\overrightarrow {a}\) và \(\overrightarrow {OK}\) theo \(\overrightarrow {b}\).
b) Biểu thị \(\overrightarrow {OM}\) theo \(\overrightarrow {a}\) và \(\overrightarrow {b}\).
Giải
a) Ta có: MH // OB, MK // OA suy ra
\(\frac{{OK}}{{OB}} = \frac{{AM}}{{AB}} = \frac{2}{3},\frac{{OH}}{{OA}} = \frac{{BM}}{{AB}} = \frac{1}{3}\)
Vì \(\overrightarrow {OH}\) và \(\overrightarrow {OA}\) cùng hướng và \(OH = \frac{1}{3}OA\) nên
\(\overrightarrow {OH} = \frac{1}{3}\overrightarrow {OA} = \frac{1}{3}\overrightarrow a \)
Vì \(\overrightarrow {OK}\) và \(\overrightarrow {OB}\) cùng hướng và \(OK = \frac{2}{3}OB\) nên
\(\overrightarrow {OK} = \frac{2}{3}\overrightarrow {OB} = \frac{2}{3}\overrightarrow b \)
b) Vì tứ giác OHMK là hình bình hành nên
\(\overrightarrow {OM} = \overrightarrow {OH} + \overrightarrow {OK} = \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b \).