+) Hệ bất phương trình bậc nhất hai ẩn là một hệ gồm hai hay nhiều bất phương trình bậc nhất hai ẩn. +) Cặp số \(({x_0};{y_0})\) là nghiệm của một hệ BPT bậc nhất hai ẩn khi \(({x_0};{y_0})\) đồng thời là nghiệm của tất cả các BPT trong hệ đó.

Ví dụ 1:

\(\left\{ \begin{array}{l}2x + 3y > 10\\x – y \le 7\end{array} \right.\);\(\left\{ \begin{array}{l}x + 3y \le 5\\x – 2y > 7\\2x > 3\end{array} \right.\)

Ví dụ 2: cặp số \((7;0)\) là một nghiệm của hệ BPT \(\left\{ \begin{array}{l}2x + 3y > 10\\x – y \le 7\end{array} \right.\)

Biểu diễn miền nghiệm của một hệ BPT bậc nhất hai ẩn: Bước 1: Trên cùng một mặt phẳng tọa độ, biểu diễn miền nghiệm của mỗi bất phương trình của hệ bằng cách gạch bỏ phần không thuộc miền nghiệm của nó. Bước 2: Phần không bị gạch là miền nghiệm của hệ BPT.

Ví dụ: Biểu diễn miễn nghiệm của hệ bất phương trình:

\(\left\{ \begin{array}{l}
2x + y \le 4\\
x + y \le 3\\
x \ge 0\\
y \ge 0
\end{array} \right.\)

Giải

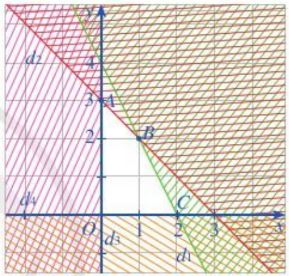
Vẽ các đường thẳng: \({d_1}:2x + y = 4;{d_2}:x + y = 3\); \({d_3}:x = 0\) là trục tung; \({d_4}:y = 0\) là trục hoành.

Gạch đi các phần không thuộc miễn nghiệm của mỗi bất phương trình.

Miễn nghiệm của hệ bất phương trình là tứ giác OABC kể cả miễn trong (còn gọi là miễn tứ giác OABC) với O(0; 0), A(0 ; 3), B(1; 2), C(2; 0).

Cho hệ BPT bậc nhất hai ẩn x, y có miền nghiệm là miền đa giác \({A_1}{A_2}…{A_n}\).

Khi đó: Giá trị lớn nhất (hay nhỏ nhất) của biể thức \(T(x;y) = mx + ny\), với \((x;y)\) là tọa độ các điểm thuộc miền đa giác \({A_1}{A_2}…{A_n}\), đạt được tại một trong các đỉnh của đa giác đó.

Ví dụ: Trong năm nay, một cửa hàng điện lạnh dự định kinh doanh hai loại máy điều hoà điều hoà hai chiều và điều hoà một chiều với số vốn ban đầu không vượt quá 1,2 tỷ đồng.

	Điều hòa hai chiều	Điều hòa một chiều
Giá mua vào	20 triệu đồng/1 máy	10 triệu đồng/1 máy
Lợi nhuận dự kiến	3,5 triệu đồng/1 máy	2 triệu đồng/1 máy

Cửa hàng ước tính rằng tổng nhu cầu của thị trường sẽ không vượt quá 100 máy cả hai loại. Nếu là chủ cửa hàng thì em cần đầu tư kinh doanh mỗi loại bao nhiêu máy đề lợi nhuận thu được là lớn nhất?

Giải

Giả sử cửa hàng cần nhập số máy điều hoà hai chiều là x và số máy điều hoà một chiều là y. Khi đó ta có \(x \ge 0,y \ge 0\).

Vì nhu cầu của thị trường không quá 100 máy nên \(x{\rm{ }} + {\rm{ }}y{\rm{ }} \le 100.\)

Số tiên để nhập hai loại máy điều hoà với số lượng như trên là: 20x + 10y (triệu đồng).

Số tiền tối đa để đầu tư cho hai loại máy là 1,2 tỉ đồng, nên ta có \(20x + 10y \le 1200\) hay \(2x + y \le 120\)

Từ đó ta thu được hệ bất phương trình bậc nhất hai ần sau:

\(\left\{ \begin{array}{l}
x \ge 0\\
y \ge 0\\
x + y \le 100\\
2x + y \le 120
\end{array} \right.\) 

Lợi nhuận thu được khi bán x máy điều hoà hai chiều và y máy điều hoà một chiều là F(x;y) = 3,5x + 2y.

Ta cần tìm giá trị lớn nhất của F(x, y) khi (x, y) thoả mãn hệ bắt phương trình trên.

Xác định miền nghiệm của hệ bất phương trình trên. Miền nghiệm là miền tứ giác OABC với toạ độ các đỉnh O(0:0), A(0;100), B(20;80) và C(60;0) 

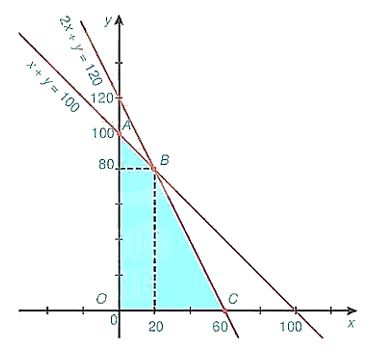
Tính giá trị của biểu thức F tại các đỉnh của tứ giác này: F (0;0) = 0, F (0;100) = 200, F (20,80) = 230, F (60;0) = 210.

 So sánh các giá trị thu được của F ở Bước 2, ta được giá trị lớn nhất cần tìm là F (20:80) = 230.

Vậy cửa hàng cần đầu tư kinh doanh 20 máy điều hoà hai chiều và 80 máy điều hoà một chiều để lợi nhuận thu được là lớn nhất.