Một tam giác hoàn toàn xác định nếu biết một trong những dữ kiện sau:

– Biết độ dài hai cạnh và độ lớn góc xen giữa hai cạnh đó:

– Biết độ dài ba cạnh;

– Biết độ dài một cạnh và độ lớn hai góc kể với cạnh đó.

Giải tam giác là tính các cạnh và các góc của tam giác dựa trên những dữ kiện cho trước.

Ví dụ: Cho tam giác ABC có AB = 6, BC = 10, CA = 14 (Hình sau). Tính số đo góc B.

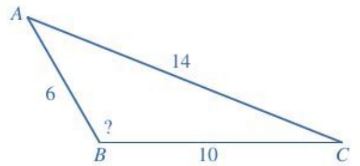
Giải

Áp dụng định lí côsin trong tam giác ABC, ta có:

\(\begin{array}{l}
\cos B = \frac{{A{B^2} + B{C^2} – A{C^2}}}{{2.AB.BC}}\\
 = \frac{{{6^2} + {{10}^2} – {{14}^2}}}{{2.6.10}} =  – 0,5
\end{array}\)

Do đó: \(\widehat B = {120^0}\)

Cho tam giác ABC có BC = a, CA = b, AB = c. Khi đó, diện tích S của tam giác ABC là: \(S = \frac{1}{2}bc.\sin A = \frac{1}{2}ca.\sin B = \frac{1}{2}ab.\sin C.\)

Ta có công thức Heron để tính diện tích tam giác theo độ dài ba cạnh của nó như sau:

Cho tam giác ABC có BC = a, CA = b, AB = c, \(p = \frac{{a + b + c}}{2}\). Khi đó, diện tích S của tam giác ABC là:

\(S = \sqrt {p\left( {p – a} \right)\left( {p – b} \right)\left( {p – c} \right)} \)

Ví dụ: Mảnh vườn hình tam giác của gia đình bạn Nam có chiểu dài các cạnh là: MN = 20m, NP = 28m, MP = 32m (hình sau). Hỏi diện tích mảnh vườn của gia đình bạn Nam là bao nhiêu mét vuông (làm tròn đến hàng phần mười)?

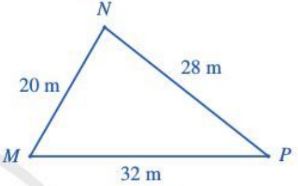
Giải

Ta có: \(p = \frac{{20 + 28 + 32}}{2} = 40(m)\)

Diện tích mảnh vườn là: 

\(\begin{array}{l}
S = \sqrt {40\left( {40 – 20} \right)\left( {40 – 28} \right)\left( {40 – 32} \right)} \\
 \approx 277,1\left( {{m^2}} \right)
\end{array}\)  

Ví dụ 1: Đứng ở vị trí A trên bờ biển, bạn Minh đo được góc nghiêng so với bờ biển tới một vị trí C trên đảo là 30°. Sau đó di chuyển dọc bờ biển đến vị trí ö cách A một khoảng 100 m và đo được góc nghiêng so với bờ biển tới vị trí C đã chọn là 40°.

Tính khoảng cách từ vị trí C trên đảo tới bờ biển theo đơn vị mét (làm tròn kết quả đến hàng phần mười). 

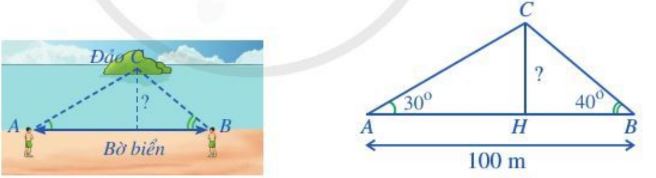
Giải

Xét tam giác ABC (Hình trên). ta có: \(\widehat C = {180^0} – \left( {{{30}^0} + {{40}^0}} \right) = {110^0}\). 

Áp dụng định lí sin trong tam giác ABC, ta có: \(\frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}.\)

Do đó: \(AC = \frac{{AB.\sin B}}{{\sin C}} = \frac{{100.\sin {{40}^0}}}{{\sin {{110}^0}}} \approx 68,4(m).\)

Xét tam giác vuông AHC, ta có: \(CH = AC.sin30^\circ  \approx 68,4.0,5 \approx 34,2\left( m \right).\) 

Vậy khoảng cách từ vị trí C trên đảo tới bờ biển khoảng 34,2 m.

Ví dụ 2: Một đường hầm được dự kiến xây dựng xuyên qua một ngọn núi. Để ước tính chiều đài của đường hàm, một kĩ sư đã thực hiện các phép đo và cho ra kết quả như Hình sau. Tính chiều đài của đường hầm tử các số liệu đã khảo sát được.

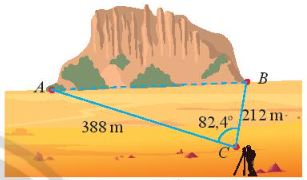
Giải

Áp dụng định lí côsin trong tam giác ABC, ta có:

\(A{B^2} = C{A^2} + C{B^2} – 2CA.CB.\cos C = 388{}^2 + {212^2} – 2.388.212.cos82,{4^0} \approx 173730\).

Suy ra: \(AB \approx \sqrt {173730}  = 417\left( m \right)\) 

Vậy đường hầm dài khoảng 417 m.