a) Định nghĩa

Số trung bình cộng của một mẫu n số liệu thống kê bằng tổng của các số liệu chia cho số các số liệu đó. Số trung bình cộng của mẫu số liệu \({x_1},{x_2},…,{x_n}\) bằng  \(\bar x = \frac{{{x_1} + {x_2} + … + {x_n}}}{n}\).

Ví dụ: Kết quả 4 lần kiểm tra môn Toán của bạn Hoa là: 7     9     8     9

Tính số trung bình cộng \(\bar x\) của mẫu số liệu trên. 

Giải

Số trung bình cộng của mẫu số liệu trên là:

\(\bar x = \frac{{7 + 9 + 8 + 9}}{4} = \frac{{33}}{4} = 8,25\)

b) Ý nghĩa

Trong thực tiễn, để tìm hiểu một đối tượng thống kê ta đưa ra tiêu chí thống kê và tiến hành thu thập nhiễu lần số liệu thống kê theo tiêu chí đó, tạo thành mẫu số liệu. Căn cứ vào mẫu số liệu đó, ta rút ra những kết luận có ích về đối tượng thống kê. Để kết luận rút ra phản ánh đúng đắn bản chất của đối tượng, ta cần nhận biết được hình thái và xu thế thay đổi của mẫu số liệu. Với cách nhìn nhận như thế, số trung bình cộng của mẫu số liệu có ý nghĩa sau:

Khi các số liệu trong mẫu ít sai lệch với số trung bình cộng, ta có thể giải quyết được vấn đề trên bằng cách lấy số trung bình cộng làm đại diện cho mẫu số liệu.

Chẳng hạn, để dự báo lượng mưa trong tháng 8 tại Hà Nội người ta tiến hành đo lượng mưa của từng ngày trong tháng 8 tại Hà Nội, ta được mẫu số liệu gồm 31 số liệu. Số trung bình cộng của mẫu số liệu đó được xem như lượng mưa trung bình tháng 8 của Hà Nội. Thống kê lượng mưa trung bình tháng 8 của Hà Nội trong nhiều năm liên tiếp sẽ cho ta những dự báo (ngày càng chính xác hơn) lượng mưa trung bình tháng 8 của Hà Nội trong những năm sắp tới.

a) Định nghĩa

Sắp thứ tự mẫu số liệu gồm n số liệu thành một dãy không giảm (hoặc không tăng). + Nếu n là lẻ thì số liệu đứng ở vị trí thứ \(\frac{{n + 1}}{2}\) (số đứng chính giữa) gọi là trung Vị. + Nếu n là chẵn thì số trung bình cộng của hai số liệu đứng ở vị trí thứ \(\frac{n}{2}\) và \(\frac{n}{2} + 1\) gọi là trung vị. Trung vị kí hiệu là \({M_e}\).

Ví dụ

a) Tính các trung vị của số sách các bạn ở Tổ 1 và số sách các bạn ở Tổ 2 đã đọc trong HĐ2.

b) Sử đụng trung vị, hãy so sánh xem các bạn ở tô nào đọc nhiều sách ở thư viện hơn.

Giải

a) Sắp xếp sô sách mỗi bạn Tô 1 đã đọc theo thứ tự không giảm, ta được đấy:

1; 1; 1; 2; 2; 2; 3; 3; 25.

Vì cỡ mẫu bằng 9 nên trung vị của Tổ 1 là số liệu thứ 5 của dãy trên, tức là \({M_e} = 2\)

Sắp xếp số sách mỗi bạn Tổ 2 đã đọc theo thứ tự không giảm. ta được đấy:

3; 3; 4; 4; 4; 4; 5; 5

Vì cỡ mẫu bằng 8 nên trung vị của Tổ 2 là trung bình cộng của sô liệu thứ 4 và thứ 5 của dãy trên, tức là \({M_e} = \frac{1}{2}\left( {4 + 4} \right) = 4\)

b) Nếu so sánh theo trung vị thì các bạn Tổ 2 đọc nhiều sách ở thư viên hơn các bạn Tổ 1. 

b) Ý nghĩa

Nếu những số liệu trong có sự chênh lệch lớn thì ta nên chọn thêm trung vị làm diện cho mẫu số liệu đó nhằm điều chỉnh một số hạn chế khi sử dụng số trung bình cộng. Những kết luận về đối tượng thống kê rút ra khi đó sẽ tin cậy hơn. 

a) Định nghĩa 

Sắp thứ tự mẫu số liệu gồm é số liệu thành một dãy không giảm. Tứ phân vị của mẫu số liệu trên là bộ ba giá trị: tứ phân vị thứ nhất, tứ phân vị thứ hai và tứ phân vị thứ ba; ba giá trị này chia mẫu số liệu thành bốn phần có số lượng phản tử bằng nhau. + Tứ phân vị thứ hai \({Q_2}\) bằng trung vị. + Nếu X là số chẵn thì tứ phân vị thứ nhất \({Q_1}\) bằng trung vị của nửa dãy phía dưới và tứ phân vị thứ ba \({Q_3}\) bằng trung vị của nửa dãy phía trên. + Nếu X là số lẻ thì tứ phân vị thứ nhất \({Q_1}\) bằng trung vị của nửa dãy phía dưới (không bao gồm \({Q_2}\)) và tứ phân vị thứ ba \({Q_3}\) bằng trung vị của nửa dãy phía trên (không bao gồm \({Q_2}\)).

Ví dụ: Hàm lượng Natri (đơn vị miligam, 1 mg = 0,001 g) trong 100 g một số loại ngũ cóc được cho như sau:

Hãy tìm các tứ phân vị. Các tứ phân vị này cho ta thông tin gi?

Giải

+ Sắp xếp các giá trị này theo thứ tự không giảm:

+ Vì n= 20 là số chẵn nên Q2 là trung bình cộng của hai giá trị chính giữa:

Q2 = (180 + 180) : 2 = 180.

+ Ta tìm Q1 là trung vị của nủa số liệu bên trái Q2:

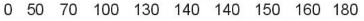
Và tìm được Q1 = (130 + 140) : 2 = 135.

+ Ta tìm Q3 là trung vị của nửa số liệu bên phải Q2:

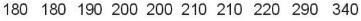
và tìm được Q3 = (200 + 210) : 2 = 205

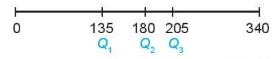
Hình ảnh về sự phân bố của mẫu số liệu

Các tứ phân vị cho ta hình ảnh phân bỗ của mẫu số liệu. Khoảng cách từ Q1 đến Q2 là 45 trong khi khoảng cách từ Q2 đền Q3 là 25. Điều này cho thấy mẫu số liệu tập trung với mật độ cao ở bên phải của Q2 và mật độ thấp ở bên trái của Q2.

b) Ý nghĩa

+ Trong thực tiễn, có những mẫu số liệu mà nhiễu số liệu trong mẫu đó vẫn còn sự chênh lệch lớn so với trung vị. Ta nên chọn thêm những số khác cùng làm đại diện cho mẫu đó. Bằng cách lấy thêm trung vị của từng dãy số liệu tách ra bởi trung vị của mẫu nói trên, ta nhận được tứ phân vị đại diện cho mẫu số liệu đó.

+ Bộ ba giá trị \({Q_1},{Q_2},{Q_3}\) trong tứ phân vị phản ánh độ phân tán của mẫu số liệu. Nhưng mỗi giá trị \({Q_1},{Q_2},{Q_3}\) lại đo xu thế trung tâm của phần số liệu tương ứng của mẫu đó.

a) Định nghĩa 

Mốt của mẫu số liệu là giá trị có tần số lớn nhất trong bảng phân bố tân số và kí hiệu là \({M_0}\).

Chú ý: Một mẫu số liệu có thể có một hoặc nhiều mốt. 

Ví dụ: Số vụ va chạm giao thông mỗi ngày tại một ngã tư được ghi lại trong bảng tần số sau:

Tìm mốt của mẫu sô liệu trên.

Giải

Số ngày có 1 vụ va chạm là 17, lớn hơn số ngày có 0, 2, 3, 4 vụ va chạm. Do đó mẫu số liệu trên có \({M_0} = 1\). 

b) Ý nghĩa

Mốt của một mẫu số liệu đặc trưng cho số lần lặp đi lặp lại nhiều nhất tại một vị trí của mẫu số liệu đó. Dựa vào mốt, ta có thể đưa ra những kết luận (có ích) về đối tượng thống kê.