Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện (các cách thực hiện của cả hai hành động là khác nhau đôi một) thì công việc đó có m + n cách hoàn thành.

Ví dụ: Bạn Phương có 7 quyển sách Tiếng Anh và 8 quyển sách Văn học, các quyển sách là khác nhau. Hỏi bạn Phương có bao nhiêu cách chọn một quyển sách để đọc?

Giải

Việc chọn một quyển sách để đọc là thực hiện một trong hai hành động sau:

Chọn một quyển sách Tiếng Anh: Có 7 cách chọn.

Chọn một quyển sách Văn học: Có 8 cách chọn.

Vậy có 7 + 8 = 15 cách chọn một quyển sách để đọc.

Nhận xét: Tương tự. ta cũng có quy tắc sau:

Một công việc được hoàn thành bởi một trong ba hành động. Nếu hành động thứ nhất có m cách thực hiện, hành động thứ hai có n cách thực hiện hành động thứ ba có p cách thực hiện (các cách thực hiện của ba hành động là khác nhau đôi một) thì công việc đó có m + n + p cách hoàn thành.

Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu hành động thứ nhất có m cách thực hiện và ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai thì công việc đó có m.n cách hoàn thành.

Ví dụ: Trong Hoạt động 1, nếu gia đình bạn Liên muốn chọn một địa điểm tham quan trong chương trình 1, sau đó đi tham quan tiếp một địa điểm trong chương trình 2 thì có bao nhiêu cách chọn hai địa điểm ở hai chương trình khác nhau để tham quan?

Giải

Việc chọn hai địa điểm ở hai chương trình khác nhau để tham quan là thực hiện hai hành động liên tiếp: chọn một địa điểm trong chương trình 1, sau đó chọn một địa điểm trong chương trình 2.

Có 4 cách chọn địa điểm tham quan trong chương trình 1.

Với mỗi cách chọn một địa điểm tham quan trong chương trình I sẽ có 7 cách chọn địa điểm tham quan trong chương trình 2.

Vậy có tất cả 4.7 = 28 cách chọn hai địa điểm tham quan ở hai chương trình khác nhau.

Nhận xét: Tương tự, ta cũng có quy tắc sau:

Một công việc được hoàn thành bởi ba hành động liên tiếp: Nếu hành động thứ nhất có m cách thực hiện; ứng với mỗi cách thực hiện hành động thứ nhất, có n cách thực hiện hành động thứ hai; ứng với mỗi cách thực hiện hành động thứ nhất và mỗi cách thực hiện hành động thứ hai có p cách thực hiện hành động thứ ba thì công việc đó có m.n.p cách hoàn thành.

Nhận vét

* Sơ đồ hình cây (Hình cho sau) là sơ đồ bắt đầu tại một nút duy nhất với các nhánh toả ra các nút bổ sung.

* Ta có thể sử dụng sơ đồ hình cây để đếm số cách hoàn thành một công việc khi công việc đó đòi hỏi những hành động liên tiếp.

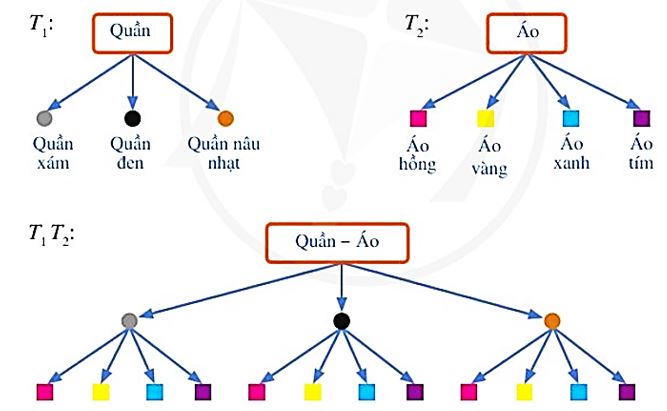
Ví dụ: Bạn Hương có 3 chiếc quần khác màu lần lượt là xám, đen, nâu nhạt và 4 chiếc áo sơ mi cũng khác màu lần lượt là hồng, vàng, xanh, tím. Hãy vẽ sơ đồ hình cây biểu thị số cách chọn:

a) 1 chiếc quần;

b) 1 chiếc áo sơ mi;

c) 1 bộ quân áo.

Giải

Các sơ đồ hình cây T₁, T₂, T₁T₂ trong Hình cho sau lần lượt:

a) Biểu thị số cách chọn 1 chiếc quần;

b) Biểu thị số cách chọn 1 chiếc áo sơ mi;

c) Biểu thị số cách chọn 1 bộ quần áo.