a) Định nghĩa

Cho \(\emptyset  \ne D \subset \mathbb{R}\) Nếu với mỗi \(x \in D\), ta xác định được y duy nhất (\(y \in \mathbb{R}\)) thì ta có một hàm số. Ta gọi: x là biến số, y là hàm số của x, D là tập xác định \(T = \left\{ {y|x \in D} \right\}\) là tập giá trị của hàm số. +) Kí hiệu hàm số: \(y = f(x),\;x \in D\)

Ví dụ:

a) Diện tích của hình tròn bán kính r được tính theo công thức \(S = \pi {r^2}\). Hỏi S có phải là hàm số của r hay không? Giải thích

b) Cho công thức y² = x. Hỏi y có phải là hàm số của x hay không? Giải thích.

Giải

a) S là hàm số của r vì mỗi giá trị của r chỉ cho đúng một giá trị của S.

b) y không phải là hàm số của x vì khi x = 1 thì ta tìm được hai giá trị tương ứng của y là 1 và -1.

b) Cách cho hàm số

– Hàm số cho bằng công thức

TXĐ của hàm số \(y = f(x)\) là tập hợp tất cả các \(x \in \mathbb{R}\) sao cho \(f(x)\) có nghĩa.

Ví dụ: \(y = \left\{ \begin{array}{l}3x + 1\quad (x \ge 1)\\5x – 1\quad (x < 1)\end{array} \right.\)

– Hàm số không cho bằng công thức.

Trong thực tiễn, có những tình huống dẫn tới những hàm số không thể cho bằng công thức. Chúng có thể được cho bằng bảng hoặc biểu đồ.

+) Hàm số \(y = f(x)\) xác định trên D, Khi đó đồ thị \((C) = \left\{ {M(x;f(x))|x \in D} \right\}\) +) Điểm \(M({x_M};{y_M})\) thuộc đồ thị hàm số \(y = f(x)\) \( \Leftrightarrow \left\{ \begin{array}{l}{x_M} \in D\\{y_M} = f({x_M})\end{array} \right.\)

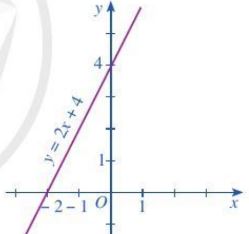
Ví dụ: Cho hàm số y= 2x + 4.

a) Vẽ đồ thị hàm số trên.

b) Trong mặt phẳng toạ độ Oxy, cho bốn điểm: A(-1; 2), B( 1; 6), C(2020; 2021), D(2030; 4064). Điểm nào thuộc đồ thị hàm số trên? Điểm nào không thuộc đồ thị hàm số trên?

Giải

a) Khi x = 0 thì y = 4; khi y = 0 thì x = – 2. Vậy đồ thị hàm số y = 2x + 4 là đường thẳng cất trục Oy tại điểm (0; 4), cắt trục Ox tại điểm (- 2 ; 0).

b) Khi x = -1 thì y = 2; khi x = 1 thì y = 6; khi x = 2020 thì y = 4044; khi x = 2030 thì y = 4064

Vậy các điểm A(- 1 ; 2), B(1 ; 6), D(2 030 ; 4 064) thuộc đồ thị hàm số và điểm C(2 020 ; 2 021) không thuộc đồ thị hàm số. 

a)  Khái niệm

+) Cho hàm số \(y = f(x)\) xác định trên khoảng \((a;b)\) – Hàm số đồng biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) < f({x_2})\) – Hàm số nghịch biến trên khoảng \((a;b)\) nếu: \(\forall {x_1},{x_2} \in (a;b),{x_1} < {x_2} \Rightarrow f({x_1}) > f({x_2})\)

+) Bảng biến thiên

Mũi tên đi xuống: diễn tả hàm số nghịch biến

Mũi tên đi lên: diễn tả hàm số đồng biến

b) Mô tả hàm số đồng biến, hàm số nghịch biến bằng đồ thị

+) Trên khoảng \((a;b)\)

– Hàm số đồng biến (tăng) thì đồ thị có dạng đi lên từ trái sang phải. 

– Hàm số nghịch biến (giảm) thì đồ thị có dạng đi xuồng từ trái sang phải.

Ví dụ: Cho hàm số y = f(x) có đồ thị như bên dưới. Quan sát đồ thị và cho biết phát biểu nào sau đây là đúng.

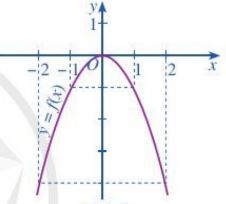
a) Hàm số y = f(x) đồng biến trên khoảng (- 2 ; – 1).

b) Hàm số y = f(x) nghịch biến trên khoảng (1 ; 2).

c) Hàm số y = f(x) đồng biến trên khoảng (- 1 ; 1).

Giải

a) Phát biểu “Hàm số y = f(x) đồng biến trên khoảng (- 2; -1)” là đúng vì đồ thị hàm số đã cho “đi lên” trên khoảng đó.

b) Phát biểu “Hàm đã y = f(x) nghịch biến trên khoảng (1; 2)” là đúng vì đồ thị hàm số đã cho “đi xuống” trên khoảng đó.

c) Phát biểu “Hàm số y = f(x) đồng biến trên khoảng (-1; 1)” là sai vì đồ thị hàm số đã cho vừa có phần “đi lên” vừa có phần “đi xuống” trên khoảng đó.