a) Hệ nhị phân

– Hệ nhị phân chỉ dùng hai chữ số 0 và 1. Mọi số đều có thể biểu diễn được trong hệ nhị phân. Nhờ vậy, có thể biểu diễn số trong máy tính.

– Hệ nhị phân có các đặc điểm sau:

+ Chỉ dùng hai chữ số là 0 và 1, các chữ số 0 và 1 gọi là các chữ số nhị phân. 

+ Mỗi số có thể biểu diễn bởi một dãy các chữ số nhị phân. 

+ Trong biểu diễn số nhị phân, một chữ số ở một hàng sẽ có giá trị gấp 2 lần chính chữ số đó ở hàng liền kề bên phải. Vì vậy chữ số 1 ở vị trí thứ k kể từ phải sang trái sẽ mang giá trị là 2^k-1

Trong hệ nhị phân, số 19 sẽ có biểu diễn là 10011. Khi cần phân biệt số được biểu diễn trong hệ đếm nào người ta viết cơ số làm chỉ số dưới như 19₁₀ hay 10011₂

b) Đổi biểu diễn số nguyên dương từ hệ thập phân sang hệ nhị phân

Biểu diễn số nguyên dương từ hệ thập phân sang hệ nhị phân

– Ta tìm các số d_k, d_k-1, …, d₁, d₀ có giá trị bằng 0 hoặc 1 sao cho

N =  d_k x 2^k + d_k-1 x 2^k-1 +…+d₁ x 2 +d₀

– Để tìm các số d_k, d_k-1, …, d₁, d₀ ta thực hiện chia liên tiếp N cho 2 để tìm số dư. Sau đó, viết các số dư theo chiều từ dưới lên ta được số nhị phân cần tìm

– Ví dụ đổi số 19 sang số nhị phân ở Hình 4.1

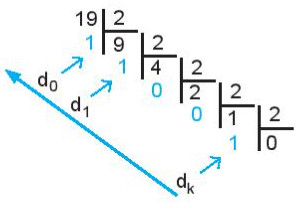
Hình 4.1. Đổi một số từ hệ thập phân sang hệ nhị phân

Số nhị phân cần tìm: 19 = 10011₂ 

Biểu diễn hệ nhị phân sang hệ thập phân

– Ta chỉ cần tính tổng của dãy d_k x 2^k + d_k-1 x 2^k-1 +…+d₁ x 2 +d₀

– Ví dụ: Đổi 10011₂ sang hệ thập phân

Số thập phân	1	0	0	1	1
Thứ tự	4	3	2	1	0

Vậy, 100112 = 1×2⁴ + 0x2³ + 0x2² + 1×2¹ + 1×2⁰ = 19

c) Biểu diễn số nguyên trong máy tính

Trong máy tính số nguyên biểu diễn bởi 1 byte (8 bít) hay 1 word (16 bít)

Biểu diễn số nguyên trong máy tính

– Số nguyên không dấu:

+ Chính là thể hiện của số trong hệ đếm cơ số 2. Khi đưa vào bộ nhớ, tuỳ theo số nhỏ hay lớn mà có thể phải dùng một hay nhiều

+ Ví dụ: Biểu diễn số 19 trong hệ đếm nhị phân có biểu diễn là 10011 chỉ cần một byte với ba bít 0 bổ sung thêm bên trái cho đủ 8 bit

19₁₀ = 00010011

– Số nguyên có dấu:

+ Cách mã hoá như mã thuận (còn gọi là mã dấu – lượng)

+ Mã bù 1 (còn gọi là mã đảo)

+ Mã bù 2.

* Lưu ý: Cả ba cách mã hoá này đều dành ra một bit tận cùng bên trái để mã hoá dấu, dấu + được mã hoá bởi bit 0, dấu – được mã hoá bởi bit 1. Số dương trong cả ba cách mã hoá này đều giống nhau, sau bit dấu (bit 0) là biểu diễn nhị phân của số. Đối với số âm thì biểu diễn của ba cách mã hoá này khác nhau.

Ví dụ: Số 19₁₀, trong cả ba cách mã hoá đều có mã là 00010011. Trong khi đó số -19₁₀ sẽ có mã thuận là 10010011, mã bù 1 là 11101100 và mã bù 2 là 11101101.

– Hệ nhị phân chỉ dùng hai chữ số 0 và 1. Mọi số đều có thể biểu diễn được trong hệ nhị phân. Nhờ vậy, có thể biểu diễn số trong máy tính. – Biểu diễn số nguyên dương trong máy tính được thực hiện một cách tự nhiên bằng cách đổi biểu diễn số sang hệ nhị phân rồi đưa vào bộ nhớ máy tính. Đối với các số nguyên có dấu, có nhiều kiểu biểu diễn khác nhau.

– Các phép tính số học trên hệ nhị phân cũng tương tự như thực hiện trên hệ thập phân.  – Do máy tính biểu diễn số trên hệ nhị phân nên máy tính cần thực hiện các phép tính số học trực tiếp trên hệ nhị phân. Vì vậy, có thể coi tính toán số học trong máy tính là ứng dụng của hệ nhị phân.

a) Bảng cộng và nhân trong hệ nhị phân

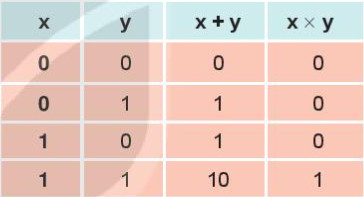
Bảng 4.1. Bảng cộng và nhân trong hệ nhị phân

* Lưu ý: 1 + 1 =10 hay nói cách khác một cộng một bằng không nhớ một 

b) Cộng hai số nhị phân

– Phép cộng cũng được thực hiện tượng tự như trong hệ thập phân, thực hiện từ phải sang trái.

– Khi phép cộng hai bit có kết quả là 10 thì ghi 0 ở hàng tương ứng dưới tổng và nhớ 1 sang hàng bên trái. Có thể xảy ra trường hợp cộng hai bịt 1 mà phải nhớ 1 từ hàng trước chuyển sang thì kết quả sẽ là 11, khi đó chúng ta ghi 1 ở hàng tương ứng dưới tổng và nhở 1 sang hàng tiếp theo bên trái.

– Hình 4.2 minh hoạ phép cộng hai số nhị phân 11011 và 11010.

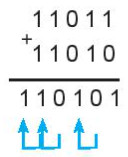
Hình 4.2. Thực hiện phép cộng

c) Nhân hai số nhị phân

– Phép nhân trong hệ nhị phân cũng được thực hiện tương tự như trong hệ thập phân.

– Ta sẽ nhận thừa số thứ nhất lần lượt với từng chữ số của thừa số thứ hai, theo thứ tự từ phải sang trái và đặt kết quả căn phải theo đúng vị trí chữ số của thừa số thứ hai, rồi cộng tất cả lại (Hình 4.3).

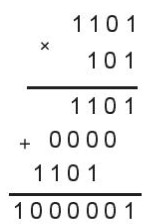
Hình 4.3. Thực hiện phép nhân