1.1. Chuyển đổi biểu diễn số ở hệ thập nhân sang hệ nhị phân
* Yêu cầu:
Chuyển số 44 ở hệ thập phân thành số ở hệ nhị phân bằng cách thực hiện theo hướng dẫn từng bước trong bảng sau:
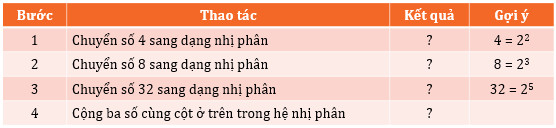
* Hướng dẫn thực hiện:
Hoàn thành bảng:
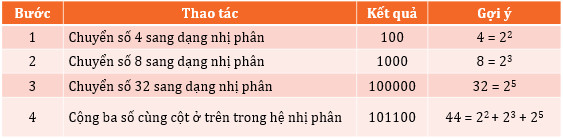
=> 44 (ở hệ 10) = 101100 (ở hệ 2)
1.2. Cộng và nhân hai số nhị phân
* Yêu cầu:
Thực hiện phép cộng và nhân hai số nhị phân. Tạo bảng (ít nhất 3 bảng) theo mẫu bên:

Ghi chú:
– Ở cột 2, hàng 1, hàng 2 là các số nhị phân tùy chọn, tương ứng với x và y mỗi số có độ dài không ít hơn 3 bit
– Trong bảng em vừa tạo ra, hãy tính và điền kết quả vào hàng 3 và hàng 4 kết quả tương ứng với phép cộng và phép nhân
* Hướng dẫn thực hiện:
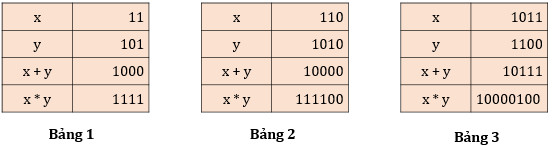
1.3. Tính số bù của một số nhị phân
* Yêu cầu:
a) Cho số nhị phân x. Kết quả của phép toán NOT x kí hiệu là \(\overline x \). Ta gọi \(\overline x \) là số bù 1 của x. Em hãy viết số bù 1 của số 44 ở hệ nhị phân.
b) Cho số nhị phân x. Kết quả của phép toán \(\overline x \) + 1 gọi là số bù 2 của x. Em hãy viết số bù 2 của số 44 ở hệ nhị phân
* Hướng dẫn thực hiện:
a) Số bù 1 của số 44 ở hệ nhị phân
44 = 101100 => số bù 1 của 44 là not (101100) = 010011
b) Số bù 2 của số 44 ở hệ nhị phân = số bù 1 của 44 + 1
= 010011 + 1 = 010100
1.4. Khám phá ý nghĩa của số bù của một số nhị phân
* Yêu cầu:
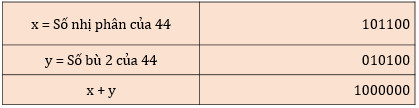
Em hãy thực hiện phép cộng số nhị phân x có giá trị thập phân là 44 với số bù 2 của x và cho biết kết quả nếu quy ước độ dài dãy bit biểu diễn số nguyên trong máy là 1 byte.
Chú ý: Với quy ước độ dài dãy bit biểu diễn số nguyên cố định trước, kết quả phép cộng x với số bù 2 của x luôn bằng 0. Số bù 2 của x cũng là số đối của x. Trong máy tính, để biểu diễn số nguyên âm, người ta không viết thêm dấu trừ mà dùng cách chuyển số nguyên nhị phân thành số bù 2.
* Hướng dẫn thực hiện: