Vật lí 11 Kết Nối Tri Thức Bài 4: Bài tập về dao động điều hòa

Cho phương trình của một vật dao động điều hòa:

\(x = 5\cos (10\pi t + \frac{\pi }{6})(cm)\)

Xác định biên độ A, tần số f, pha ban đầu \(\varphi \), và li độ x₁ tại thời điểm t₁ = 0,05s.

Giải:

So sáng phương trình dao động của vật với phương trình dạng cơ bản \(x = A\cos (\omega t + \varphi )\):

Ta có:

• Biên độ A = 5 cm
• Tần số \(f = \frac{\omega }{{2\pi }} = \frac{{10\pi }}{{2\pi }} = 5Hz\)
• Pha ban đầu \(\varphi  = \frac{\pi }{6}(rad)\)
• Li độ lúc t₁:

\({x_1} = 5\cos (10\pi .0,05 + \frac{\pi }{6}) = 5\cos (\frac{{4\pi }}{6}) =  - 2,5cm\).

Một vật dao động điều hòa với tần số 2 Hz. Tại thời điểm ban đầu vật có li độ x = 5 cm và vận tốc v = -30 cm/s. Xác định:

a) Biên độ và pha ban đầu của dao động.

b) Giá trị cực đại của vận tốc và gia tốc của vật khi dao động.

Giải:

a) Tần số góc của dao động: \(\omega  = 2\pi f = 4\pi (rad/s).\)

Khi \(t = 0\left\{ {\begin{array}{*{20}{c}}
{{x_0} = A\cos \varphi  = 5cm}\\
{{v_0} =  - \omega A\sin \varphi  =  - 30cm/s}
\end{array}} \right.\)

Biên độ và pha ban đầu của dao động:

\(A = \sqrt {{x^2} + \frac{{{v^2}}}{{{\omega ^2}}}}  = \sqrt {{5^2} + \frac{{{{( - 30)}^2}}}{{{{(4\pi )}^2}}}}  \approx 5,54cm\)

\(\tan \varphi  = \frac{{\omega {x_0}}}{{{v_0}}} = \frac{{30}}{{4\pi .5}} = \frac{3}{{2\pi }} \Rightarrow \varphi  \approx 0,44rad\)

b) Vận tốc cực đại của vật: \({v_{\max }} = \omega A = 4\pi .5,54 \approx 70cm/s.\)

Gia tốc cực đại của vật: \({a_{\max }} = {\omega ^2}A = {(4\pi )^2}.5,{54.10^{ - 2}} \approx 8,8m/{s^2}.\)

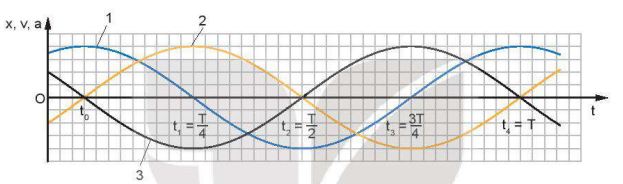
Một vật dao động điều hòa với tần số góc \(\omega  = 1\) rad/s, có đồ thị của li độ x, vận tốc v và gia tốc a theo thời gian t được mô tả trên Hình 4.1.

Hình 4.1

Hãy chỉ đúng đồ thị của li độ (x - t), vận tốc (v - t), gia tốc (a - t) theo thời gian t trên Hình 4.1.

Giải:

Ta đã biết:

- Vận tốc v sớm pha \(\frac{\pi }{2}\) so với li độ và trễ pha \(\frac{\pi }{2}\) so với gia tốc.

- Gia tốc a ngược pha so với li độ và sớm pha \(\frac{\pi }{2}\) so với vận tốc.

Do đó, trên Hình 4.1 đường 2 là đồ thị li độ x(t), đường 1 là đồ thị vận tốc v(t), đường 3 là đồ thị gia tốc a(t).